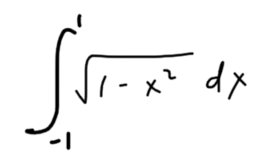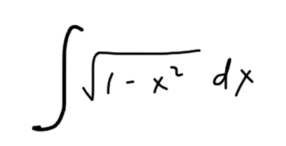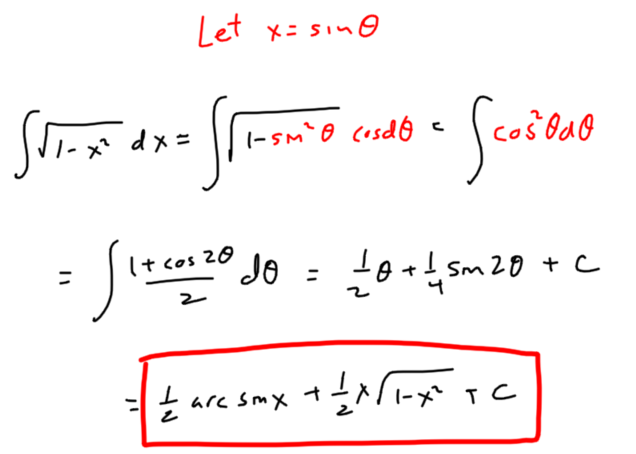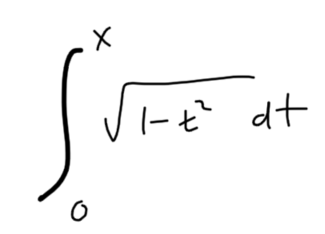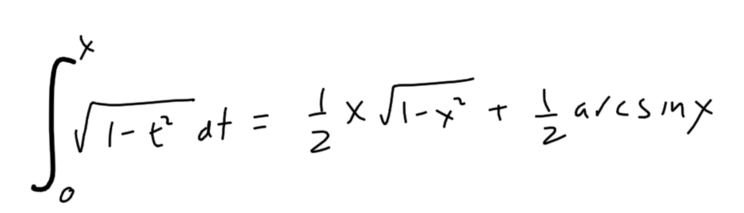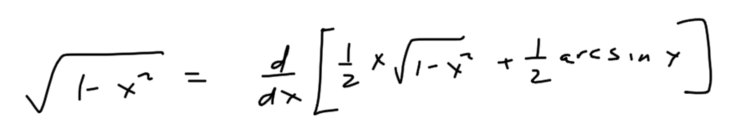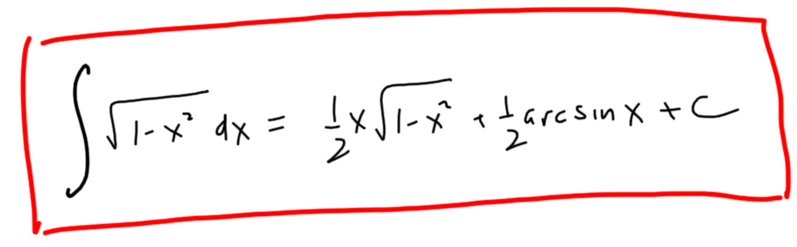Geometry

Teaching Triangle Angle Sum

The Triangle Angle Sum Theorem is one of my favorite topics in Geometry class. It’s a foundational fact about triangles, and in geometry, every problem is a problem about triangles.

I love the standard proof of the theorem, where a line is constructed through a vertex that is parallel to the opposing side. It highlights the crucial role that parallel lines play in our conception of geometry, and it points to the assumptions we make about them as well. With a little nudge, this standard proof is eminently discoverable, and makes for a great classroom activity.

But I also love showing students some non-standard proofs of the theorem. Here’s a demonstration I built in Geogebra meant to mimic a paper folding activity that shows how the angles of a triangle form a straight line.

You should do it with actual paper, too! Here’s a short video. Stick around for the bonus tearing at the end!

Apart from being fun and surprising, what I like about these demonstrations is how they illuminate something important and essential about result: It’s the straight line, not the number 180, that’s important. Plus, the tearing activity works with more than just triangles! Unfortunately it’s not so adaptable to spherical geometry, but that’s another lesson.

Related Posts

By MrHonner, 2 years2 years ago

Geometry Teaching

Who Needs Trig Sub?

As a calculus teacher, this is one of my favorite integrals.

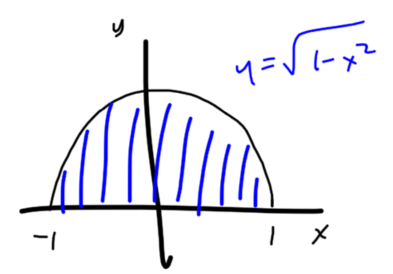
This calculation is a fun challenge for students who are so deep into integration techniques they’ve forgotten that not every integral requires antidifferentiation. It’s hard to apply the Fundamental Theorem of Calculus here because the integrand has no obvious antiderivative. But the integral is easy to compute, because it represents the area of a semicircle of radius 1.

The area, and thus the integral, is 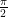$\frac{\pi}{2}$ .

I bring this integral back later in the course to motivate the technique of trigonometric substitution.

If you can’t imagine the antiderivative of the integrand the FTC isn’t much help. That’s where a clever (if complicated) change of variables, together with a few trigonometric identities, comes in. Trig substitution solves the algebraic puzzle of integrating the square root of a difference.

But when I taught this topic this year something unexpected happened.

As usual, I presented students with the indefinite integral, expecting it to be inaccessible with their current tools. This would motivate the need for a new technique, and trig substitution would come to the rescue!

But two students didn’t need rescuing. Instead, they figured out a way to evaluate this integral using tools they already had. They did what I often encourage them to do, but in an ingenious way I never would have anticipated: They turned this indefinite integral into an area problem and used geometric reasoning to evaluate it!

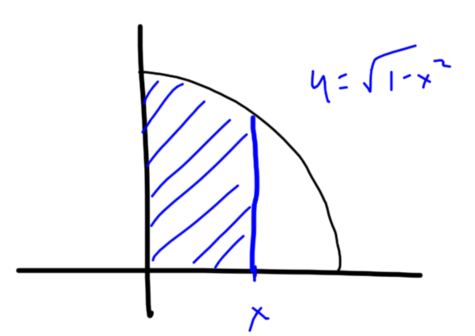
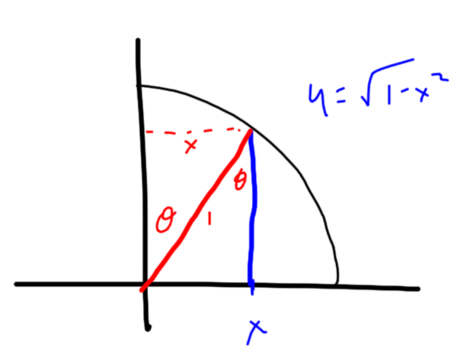
They started by reimagining the indefinite integral as a definite integral.

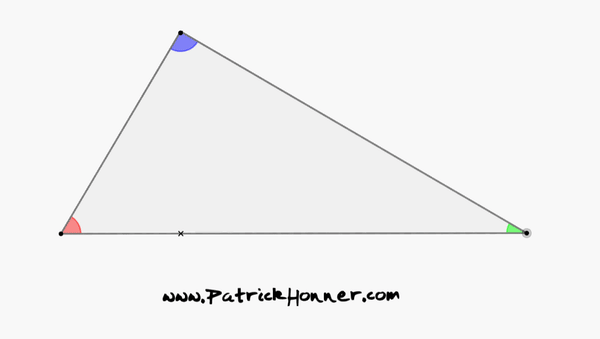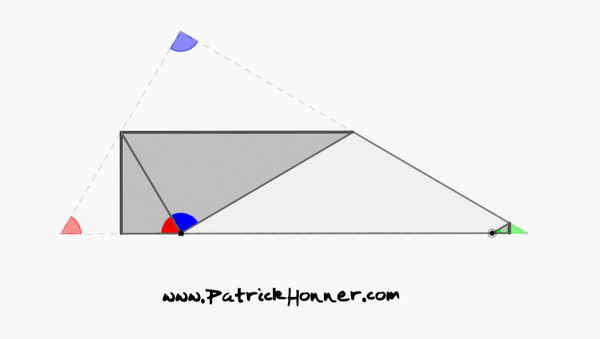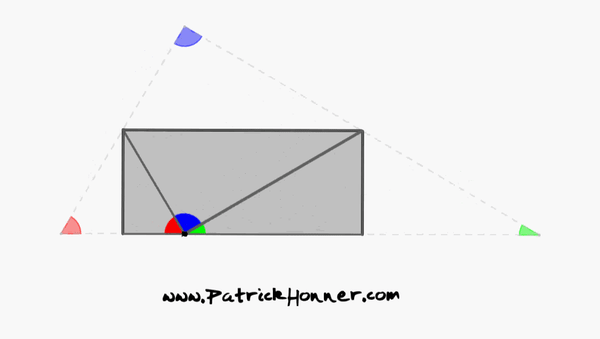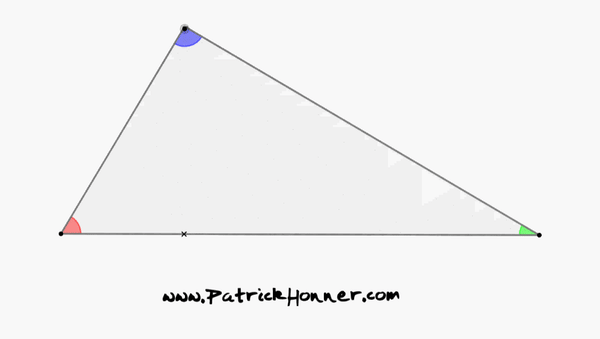
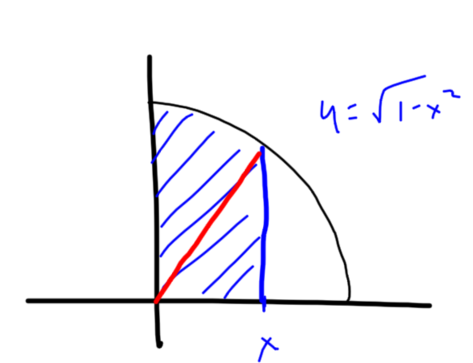
Now here’s the region whose area is given by this definite integral.

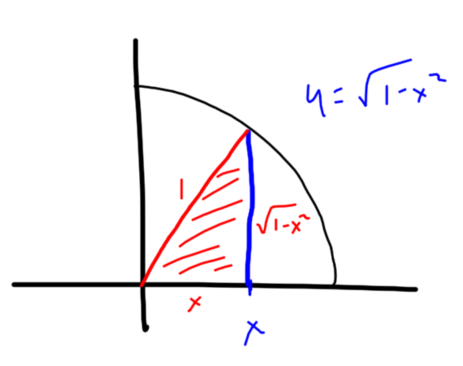
The region can be thought of as a right triangle and a sector of a circle.

Because the circle has radius 1, the sides of the triangles are $x$ and $\sqrt{1-x^2}$ .

Which makes the area of the triangle 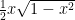$\frac{1}{2} x\sqrt{1-x^2}$ .

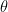Now the area of a circular sector is equal to $\frac{\theta}{2\pi} \pi r^2$ , where $\theta$ is the central angle. In our diagram

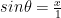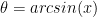we have $sin\theta = \frac{x}{1}$ , so $\theta = arcsin(x)$ . Since the radius of the circle is 1, the area of the circular sector is

$\frac{1}{2\pi}\pi arcsin(x) = \frac{1}{2}arcsin(x)$

The area of the entire region is then the sum of the areas of the triangle and the sector. But the area is also the value of the definite integral. So they must be equal!

Differentiating both sides (thanks again to the FTC) shows that we really have found an antiderivative of $\sqrt{1-x^2}$ , as required.

And so

Which of course, is the same result we find using trig substitution.

I’ve taught this topic for many years and never thought of this approach. I’m grateful to have learned something new from my students, who never fail to impress me with their creativity. And I’m glad I gave them time and space to solve what I thought was an impossible problem! When I teach this next time, I’ll be sure to do it again. And I’ll be sure to share this ingenious integration.

UPDATE: I’ll also be sure to show them this other ingenious solution that a different student came up with!

Related Posts

By MrHonner, 3 years3 years ago

Geometry Resources Writing

The Crooked Geometry of Round Trips — Quanta Magazine

My latest column for Quanta Magazine explores what round-the-world trips would look like if we didn’t live on a sphere.

Have you ever wondered what life would be like if Earth weren’t shaped like a sphere? We take for granted the smooth ride through the solar system and the seamless sunsets afforded by the planet’s rotational symmetry. A round Earth also makes it easy to figure out the fastest way to get from point A to point B: Just travel along the circle that goes through those two points and cuts the sphere in half. We use these shortest paths, called geodesics, to plan airplane routes and satellite orbits.
But what if we lived on a cube instead? Our world would wobble more, our horizons would be crooked, and our shortest paths would be harder to find.

Classification of geodesic paths on platonic solids didn’t happen until relatively recently, and the case of the dodecahedron offers quite a surprise! To learn more, read the full article here.

By MrHonner, 3 years3 years ago

Geometry Photography

Math Photo — Parallel Paths

I like the parallel paths traveling across the surface of this lampshade. I can’t recall ever seeing this irregular polyhedron before, with its equatorial belt of alternating isosceles triangles and trapezoids at the top and bottom.

By MrHonner, 4 years4 years ago

Geometry Resources

How Simple Math Can Cover Even the Most Complex Holes — Quanta Magazine

My latest column for Quanta Magazine starts with a simple question: If you had a cover a hole that was at most 1 inch wide, what kind of patch would you need?

This problem is related to Lebesgue’s universal covering problem: The goal is to find the smallest such patch that could cover any hole of diameter one. After 100 years mathematicians still don’t have a full answer, but some techniques from high school geometry are getting us closer.

By starting with known covers, we can chop off pieces we can prove we don’t need, and make our covers smaller and smaller.

Read the full article for more, which is freely available in Quanta Magazine.