Who Needs Trig Sub? Part 2
I recently wrote about an ingenious integration performed by two of my students. But that wasn’t the whole story. Here’s the rest.
It begins with this integral.
Usually when challenged to evaluate this integral students will try a few substitutions, fail to find an antiderivative, and realize something new is needed. This sets the stage for trigonometric substitution, which we then use to untangle the algebraic obstacles in the integrand.
But this was an unusual year. Not only did two students surprise me with a purely geometric approach, a third student found another completely different solution I had never seen before. She used integration by parts!
This application of integration by parts leads to the following equation.
Which she simplified to this.
This is the point where I would probably abandon integration by parts, because it doesn’t look the situation has improved. But my student did something incredibly inspired. She rewrote the integral
like this
And this is definitely an improvement. The integral on the right is known: it’s just . And the other integral is the one we were trying to find in the first place. When this is substituted back into the integration by parts equation you get this
The integral we want to evaluate is now on both sides of the equation, so just collect like terms and solve
Before this year I had never seen any alternate derivation of this formula. This year students produced two completely new ones!
I can understand why students had never attempted this technique before. Integration by parts typically comes after trig substitution in the course, so it wouldn’t usually be an option for them. But this year, because of the way I rearranged the curriculum, integration by parts came first. And I’m thrilled that my student thought to try it. And persevered!
It also made me feel good about my integration by parts lesson. Usually the last problem I present in that lesson is the integral
But this year I almost didn’t. This problem requires repeated integration by parts and quite a bit of perseverance to solve. At the end of a long lesson I considered passing on it, but we pushed through. And it was worth it! Seeing this technique set up my student to find her own ingenious integral. And to teach me something new.
Related Posts
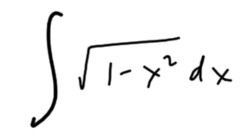
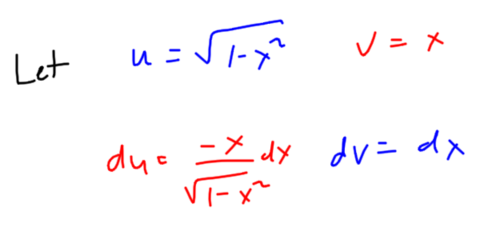

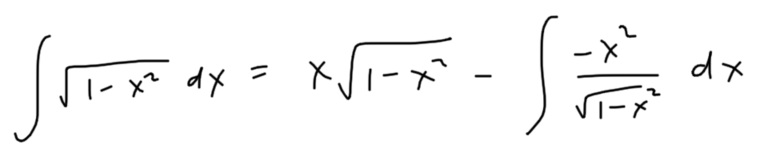
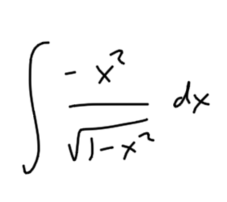
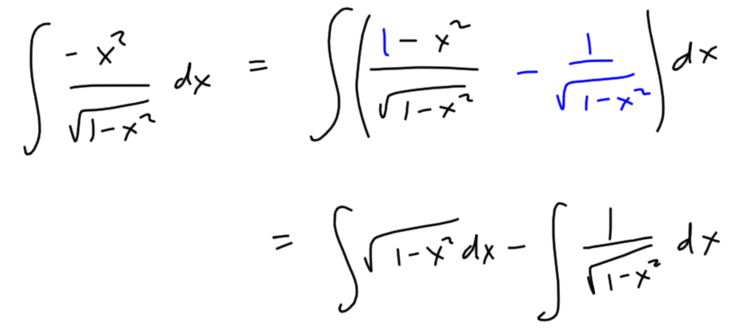
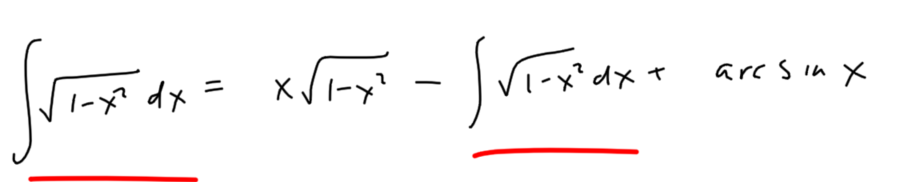
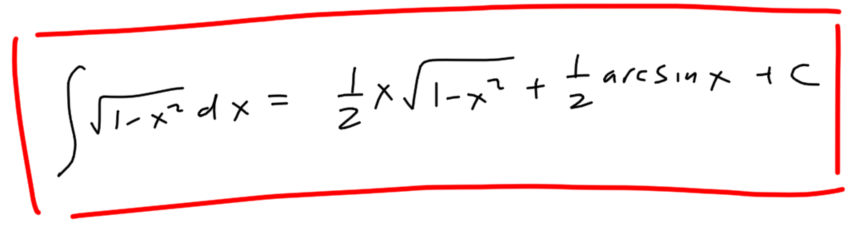
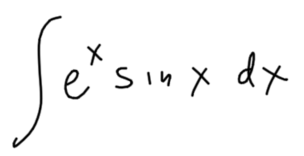
0 Comments