This menacing creature is Glyptotherium texanum. Well, was Glypotherium texanum.
The armor caught my attention. It’s made of small plates that create an interesting tiling of a curved surface.
Notice how the tiles slowly change from quadrilaterals to pentagons to hexagons, and back again! I wonder what factors determine the shape of each tile as they grow.
I’ve always enjoyed playing around with pinscreens, but only recently did I realize what cool mathematical concepts they display!
For example, the image above shows an approximation of the volume of a hemisphere using right cylinders. A pinscreen Riemann sum!
And the images below suggest how we might approximate the areas of a circle and a square using pinscreens.
Compute the ratio of raised pins to total pins, and multiply by the total area of the pinscreen. A pinscreen Monte Carlo method!
Any other cool math hiding in there?
It took several hundred encounters with this park bench before I realized it was a heptagon! I don’t see many regular, seven-sided figures in my experience, which made this a surprising discovery. I wonder what prompted this design choice.
Like most real-world instances of perfect geometric objects, it doesn’t exactly measure up. But what’s a few degrees between n-gons?
Looking through this system of parallel curves makes me think about the many different ways we can impose coordinate systems on spaces. An ordered pair of coordinates specifies a unique location on this curved surface just as a pair 
This image also reminds me of the role of context in geometry. From our perspective, this coordinate system looks curved, but if we lived on this surface, it would all seem perfectly flat! Maybe our world looks really curved to someone standing outside it.
In class, and on Twitter, I posed a question that led to lots of great conversation.
To increase the volume of a cylinder, is it better to increase the radius or the height? Great conversation starter today.#math #mathchat
— Patrick Honner (@MrHonner) January 9, 2015
There are many reasons I love this particular question. It’s familiar, accessible, and usually counter-intuitive. And it bridges algebra and geometry in a very natural way.
A reasonable response is to argue that an increase in radius will be better. The volume of a cylinder is 
If you imagine the grey cylinder shown below, this argument seems to make sense. Increasing the height a little bit adds a small blue disk of volume to the top, but increasing the radius a little bit adds a large blue shell. The additional volume of the shell clearly appears to be more than that of the disk.
However, this argument is a lot less convincing if you imagine a different cylinder.
It’s not obvious which additional volume here is larger, which suggests some further thinking is in order. At this point, some multidimensional extreme-case thinking usually leads to an appropriate conclusion: Namely, that the answer depends on the dimensions of the cylinder.
This problem is my standard introduction to partial derivatives. It creates great context for computing and comparing
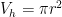
But its versatility is another reason I like this problem so much. Geometry and Calculus students can both engage in this problem in a meaningful way, using the tools available to them to analyze the situation. And it always results in great conversations!
