Geometry

3D Printing Geometry Teaching

Cavalieri’s Principle and 3D Printing

These 3D printed objects served as an excellent starting point for a classroom conversation on Cavalieri’s Principle.

Each shape above is an extrusion of the same square. In the middle, the square moves straight up; at left, the square travels in a complete circle from bottom to top; and at right, the square moves along a line segment and back.

The objects all have the same height. Since at every level they have the same cross-sectional area, by Cavalieri’s Principle they all have the same volume!

Cavalieri’s Principle is a simple but powerful idea, and one that can be easily demonstrated around the house. Here are some other examples using CDs and CD cases.

By MrHonner, 10 years10 years ago

3D Printing Appreciation Geometry

3D-Printed Chmutov Surface

My most successful 3D print so far: a Chmutov surface!

Chmutov surfaces are algebraic surfaces that have interesting properties involving their singular points. This surface has equation

$2[x^2(3-4x^2)^2 + y^2(3-4y^2)^2 + z^2(3-4z^2)^2]=3$

And in addition to being quite beautiful, this Chmutov surface is already coming in handy!

By MrHonner, 10 years10 years ago

Geometry Teaching

Sum of Angles in Star Polygons

Futility Closet recently posted a nice puzzle about the sum of the angles in the “points” of a star polygon.

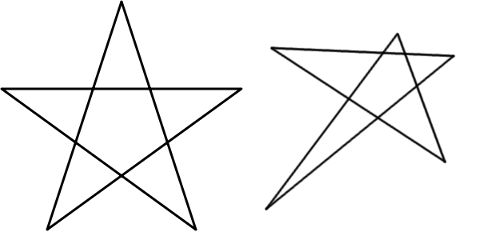
It’s easy to show that the five acute angles in the points of a regular star, like the one at left, total 180°.

Can you show that the sum of these angles in an irregular star, like the one at right, is also 180°? (link)

A clever proof is shown, but what I would consider the standard proof is clever, simple, and beautifully generalizable.

Consider the star pentagon below.

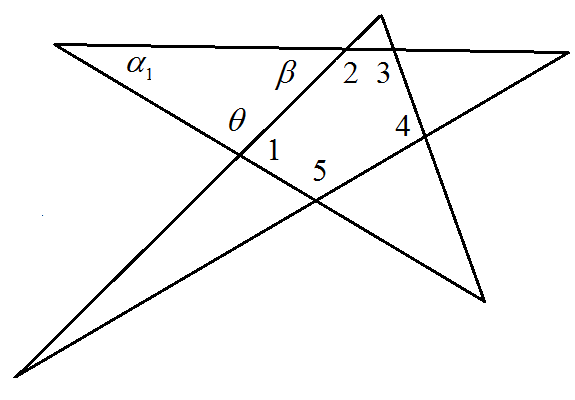By the exterior angle theorem, we have

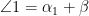
$\angle 1 = \alpha_1 + \beta$

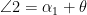
$\angle 2 = \alpha_1 + \theta$

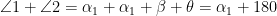
$\angle 1 + \angle 2 = \alpha_1 + \alpha_1 + \beta + \theta = \alpha_1 + 180 \textdegree$

where the last equality follows from the triangle angle sum formula.

Do this for each of the five “points” and sum the equations

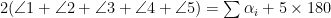
$2( \angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5) = \sum \alpha_i + 5 \times 180 \textdegree$

Now, the sum of the interior angles of any pentagon, regular or not, is 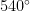$540 \textdegree$ , so this becomes

$2 \times 540 \textdegree = \sum \alpha_i + 5 \times 180 \textdegree$

And so, a little arithmetic gives us

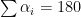
$\sum \alpha_i = 180 \textdegree$

For stars of this type, where the points are formed by intersecting two sides of an n-gon that are separated by exactly one side, this method generalizes beautifully. The above equation becomes

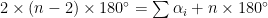
$2 \times (n-2) \times 180 \textdegree = \sum \alpha_i + n \times 180 \textdegree$

which simplifies to

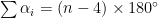
$\sum \alpha_i = (n-4) \times 180 \textdegree$

In particular, we see that when n = 5, we have that 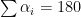$\sum \alpha_i = 180 \textdegree$ . And one of the best things about having a formula like this is asking questions like “What happens when n = 4?” and “What happens when n = 3?”!

Now, there are other types of star polygons. For example, if you start with an octagon, extend the sides, and consider the intersections of two sides that themselves are separated by exactly two sides of the octagon, you get something that looks like this.

While the formula above doesn’t apply to this star, a similar technique does. The big difference is that, instead of the star’s points being attached an an n-gon (a pentagon, in the first example), this star’s points are attached to another star polygon! There are lots of fun directions to go with this exploration.

By MrHonner, 10 years9 years ago

Art Geometry Photography

Math Photo: Bond Angles

I love the way the struts of this structure come together and align with the geometry of the city.

By MrHonner, 10 years10 years ago

Challenge Geometry

When do Multiple Rotations Exist?

I recently profiled an erroneous high-stakes math exam question that had two correct answers.

Here, it is possible to map AB onto A’B’ using either a glide reflection or a rotation.

It’s interesting to note that there are actually two distinct rotations that map AB onto A’B’, as demonstrated below.

This raises an interesting question: given two congruent objects, under what circumstances will two distinct rotations exist that map one onto the other?

In a comment on the original post, Joshua Greene offered another interesting follow-up question:

Under what circumstance, if any, are two line segments of equal length not images of each other under rotation? In which of those cases, if any, are the two line segments images of each other under glide reflection?

With enough work, even erroneous exam questions are redeemable!

By MrHonner, 10 years10 years ago

Follow Mr Honner