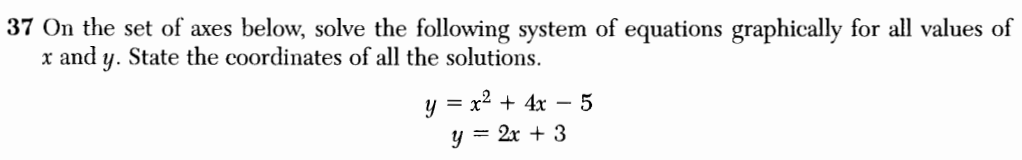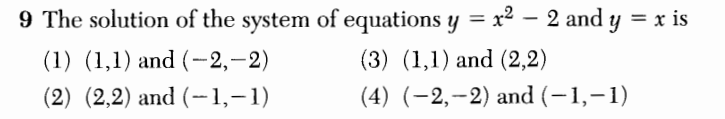MrHonner

Pi Day 2014

I don’t usually celebrate Pi Day, but a variety of inspirations intersected at a fun project idea this time around.

Thanks to Math for America, I participated in a terrific workshop on Zometool earlier this year, led by George Hart.  We built, explored, conjectured, proved, and collaborated around a lot of rich mathematical ideas.  And this semester, Steven Strogatz is teaching a History of Math course at Cornell, and he has been generously sharing thoughts and resources online.  As a result, I have been reading up on the derivations of the volume and surface area formulas for Platonic and Archimedean solids.

So when I recently re-watched James Tanton’s brilliant video “What is Pi for a Square?“, the idea hit me:  for Pi Day, students could explore the value of “Pi” for various Zometool-constructible solids!

pi day combo

What makes James Tanton’s exploration so wonderful is that it highlights the invariance of Pi in circles (as circumference by diameter) while inviting students to play around with the notions of “diameter” “radius”, and “Pi” in regular polygons.  We’ll be taking the question “What is Pi?” up a dimension, and thanks to Zometool, we have a tangible context for our conversations and calculations.

We’ll be exploring properties of polyhedra, calculating areas, volumes and ratios, arguing about definitions, and comparing the sphereness of various things.  I’m looking forward to a great day of mathematics!  And perhaps discovering what the value of “Pi” is for a rhombic triacontahedron.

By MrHonner, ago

Aftermath — Steven Strogatz on Math Education

strogatz smallAs part of our conversation in the February 2014 issue of Math Horizons, Steven Strogatz shared his thoughts on the current state of math education in the Aftermath section of the magazine.

Here’s the beginning of his “I have a dream” speech about math teaching.

In my dream world, everyone would have the chance to be a teacher the way Mr. Joffray [Strogatz’s high school calculus teacher and the subject of his book The Calculus of Friendship] was a teacher.

His job was to teach us calculus, but he had his own vision of how to teach it and he followed that vision. He was creative, and he put his personal stamp on the course for us. He trusted his judgment, and the school trusted him. He could teach us the way he wanted to teach us, and he was a great teacher.

Math Horizons makes Aftermath freely available online, so you can read the entire segment here.

By MrHonner, ago

Regents Recap — January 2014: Systems of Equations

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

Solving systems of equations is a fundamental mathematical skill.  Systems come up in a variety of mathematical contexts, and so they play a natural role in all high school math courses.

It’s not surprising, then, that solving systems of equations appear on all New York math Regents exams.  But what is surprising is how similar the questions on different exams are, given that the three exams span 3-4 years of mathematical learning.

For example, here is a problem from the Integrated Algebra exam.

2014 Int Alg Regents 37

Here is a problem from the Geometry exam.

2014 Geo Regents 9

And here is a problem from the Algebra 2 / Trig exam.

2014 Alg 2 Trig Regents 31

The question from the Integrated Algebra exam is actually harder than the question on the Geometry exam.  Ironically, the directive on the algebra exam is to solve the equation graphically.

The system on the Algebra 2 / Trig exam involves rational expressions and a quadratic equation, but these are skills students are supposed to have in the Integrated Algebra course, which they take 2-3 years earlier.

I have written about this phenomenon before, but it continues to strike me as odd that over the span of 3-4 years of mathematics instruction, this is the growth these tests are looking for.

By MrHonner, ago
Follow

Get every new post delivered to your Inbox

Join other followers: