A question from the January 2014 Integrated Algebra Regents exam asks students to identify a graph showing exponential decay. This graph was the correct choice.
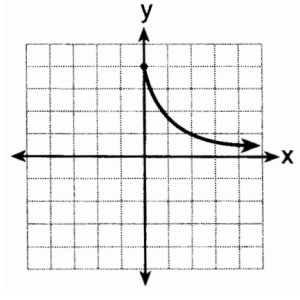
We regularly see terrible graphs on these exams: non-trigonmetric trig functions, functions intersecting their vertical asymptotes, and unscaled coordinate systems. So it comes as no surprise that this graph is not actually the graph of an exponential function!
First, note that all exponential functions have the form  . Since this graph passes through the point (0,4), we immediately see that
. Since this graph passes through the point (0,4), we immediately see that 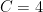 .
.
Note also that the graph passes through the point (2,1). Thus, 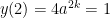 . We can now use this information to compute
. We can now use this information to compute  .
.
Since  , we see
, we see  . But
. But  , and so
, and so 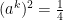 .
.
Taking the square root of both sides, we see that  . Assuming
. Assuming 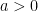 , we have
, we have  , and so
, and so  . But
. But 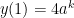 , so we now know that
, so we now know that 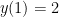 .
.
Notice, however, that the graph does not pass through the point (1,2)! Thus, this is not the graph of an exponential function.
Related Posts




