Here’s a fun challenge suggested by Matt Henderson: can you find a mathematical model for the path of a bolt of lightning?
You can check out this video of a lightning strike to get the ideas flowing:
http://www.youtube.com/watch?v=2XwFF5idD_0
The tree structure suggests graph theory, the bifurcations suggest dynamical systems, and the inherent physics suggest that some complicated differential equations might be involved.
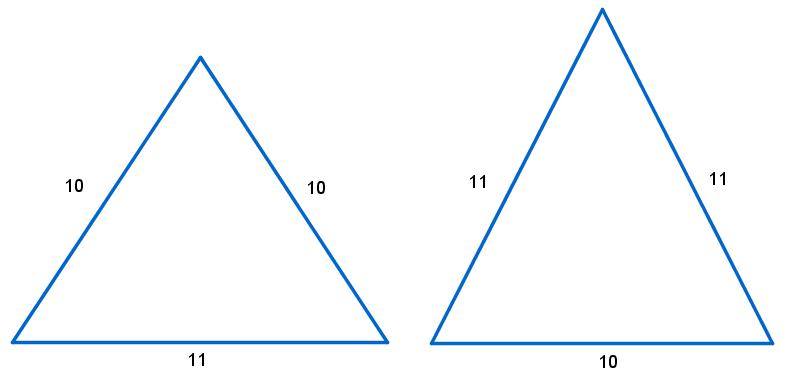
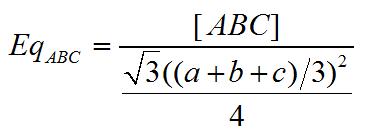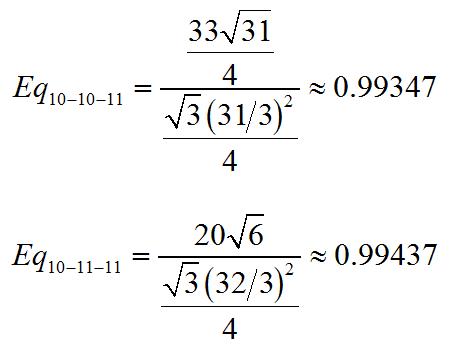A surprising amount of interest was generated by my question “Which Triangle is More Equilateral?” With the passing of consecutive Isosceles Triangle days, I wondered: which triangle was more equilateral, the 10-10-11 triangle, or the 10-11-11 triangle?
Many rich and interesting conversations arose as a result of this question. Colleagues, students, and commenters on the original post offered good ideas about how to approach both the question itself and the concept in general.
There is a lot to say about this seemingly simple problem, but I’ll begin by sharing my approach to the question “Which triangle is more equilateral?”
After playing around with several ideas, I tried to get to the heart of equilateralness. Equilateral is a well-defined idea (all sides congruent), but how could we relax that definition and quanitfy equilateralness in a continuous, rather than a discrete, way?
I chose to to think of equilateralness as a measure of how circle-like the object is: the more it’s like a circle, the more equilateral that object is. What does it mean to be circle-like? I chose the following idea as my foundation: the fundamental characteristic of the circle is that it maximizes area for a given perimeter. From that perspective, I created a measurement.
I define a triangle’s equilateralness to be the ratio of its area to the area of the equilateral triangle with the same perimeter. Thus, for triangle ABC with sides a, b, and c, its equilateralness is given by
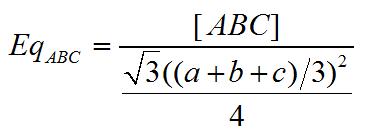
where [ABC] denotes the area of triangle ABC.
Since the equlateral triangle is the triangle of maximum area for a given perimeter, the above measure will be bewtween 0 and 1 for all triangles. The closer its Eq is to 1 , the closer the triangle is to being equilateral.
So for the triangles in question, we have
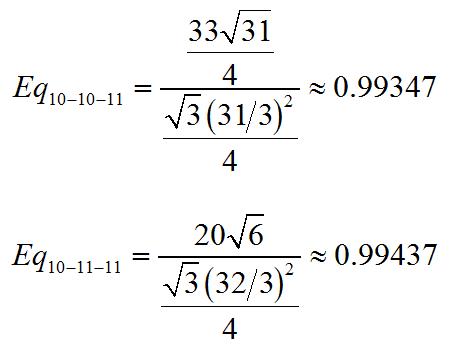
Thus, by a very slim margin, the 10-11-11 triangle is more equilateral than the 10-10-11 triangle!
The value in this question is not so much settling on this, or any, particular approach; what’s valuable here is the opportunity to creatively explore a lot of interesting and deep mathematical ideas. I look forward to doing just that!
Related Posts
As someone who is both quantitative and skeptical by nature, I always head straight for the fine print of a deal: that’s usually where you discover that it’s not as great as advertised.
Which makes the fine print here all the more confusing. I saw “You Pay 2 $3” in big font and thought to myself “Ok, I’m getting two green peppers for three dollars”.
Upon closer inspection, I realized that the price was actually two pounds of green peppers for three dollars. At around half-a-pound each, this means you really get about 4 green peppers for $3. Isn’t that what you want to advertise?
I wonder how many people picked up a green pepper, thought “$1.50 is too much!” and put it down.
Two consecutive isosceles triangle days (10/10/11 and 10/11/11) got me thinking: Which of the following triangles is more equilateral, the 10-10-11 triangle, or the 10-11-11 triangle?
Or perhaps I should say equilateraler?
[Update: here is my first attempt to answer this question in a mathematically sensible way.]
Related Posts
