Another Equilateral Comparison
The passing of consecutive isosceles triangle days has me once again thinking about the question “Which Triangle is More Equilateral?”
I first considered the question on 10/10/11, comparing the 10-10-11 triangle and the 10-11-11 triangle. After a spirited discussion, I offered one approach to the question here. The problem gave me lots to think about, both mathematically and pedagogically, and I reflected on what I liked about this problem here.
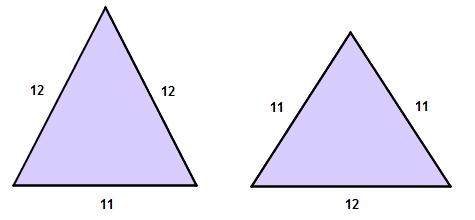
But as 12/11/11 and 12/12/11 pass, I thought I’d revisit my strategy for answering the question “Which triangle is more equilateral?”
My basic strategy, outlined in more detail here, is to ultimately to quantify the circleness of each triangle. To me, being equilateral is all about trying to be as much like a circle as possible. So I created a measure to determine how close to circlehood a triangle is. Here are the numbers.
The 11-12-12 triangle’s measure is closer to 1, thus making it the more equilateral triangle.
Related Posts
- Which Triangle is More Equilateral?
- Which Triangle is More Equilateral? Part II
- Which Triangle is More Equilateral? 2012 Edition
- An Ode to Equilateralism
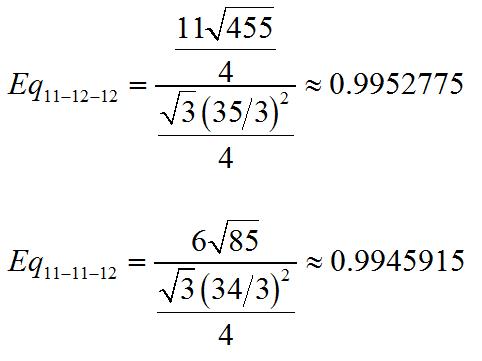
2 Comments
Roy Wright · December 12, 2011 at 10:47 am
Good stuff. I think this sort of thinking — inventing a metric to quantify something where there are multiple reasonable possibilities — is both a valuable skill in modern life, and a potentially fertile ground for developing deep mathematical understanding (along with creativity). But like just about any topic in mathematical science that is open to personal preference, discussion, and trade-offs, it’s heavily underemphasized. It’s exciting to see, in the comments on your October post, alternative metrics being introduced and discussed, especially when they are seemingly simpler but make less aesthetic sense.
MrHonner · December 12, 2011 at 6:47 pm
You have enumerated many of the virtues of this problem, which I also appreciated myself (I discussed these, and others, here).
The creativity inherent in all mathematical processes is highly under-emphasized at all levels. And it’s such a draw for students!