A palindrome is a number (or word) that reads the same forward as backward.
What’s especially nice about this palindrome is that it’s still a palindrome when you rotate it 180 degrees!
Representation
Wind Map
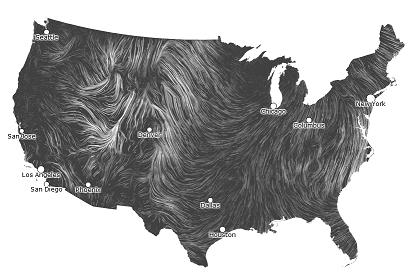This is a stunningly beautiful visualization of wind patterns in the US:
Not only is this a functional and immediately accessible representation of data, but it also brings to life the mathematical concepts of vector fields and flow lines.
Apart from atmospheric science questions like “Why is this area windier than others?” are purely mathematical questions like “Which location is the calmest?” and “Which location is most volatile?”
And if you enjoy this, be sure to check out this visualization of the world’s ocean currents!
Application
Fighting Crime with Mathematics
This is an interesting article about a young mathematician who is using techniques from seismology to build crime-prediction models.
http://www.wmbfnews.com/story/13492456/man-uses-math-to-thrwart-crime
The basic idea is that crimes are more likely to be committed in geographical clusters, much like how afterschocks of earthquakes occur around the epicenter of the original quake. Such patterns have already been identified in burglaries and gang violence.
By looking at the data from crime reports and 911-calls, better predictions can be made about where and when crimes might occur. That way resources–police officers, in particular–can be deployed more efficiently.
Uncategorized
Statistical Baseball Predictions
As the 2012 Major League Baseball season gets under way, it’s a good time to check in on the predictions of Bruce Bukiet, mathematics professor at the New Jersey Institute of Technology.
http://m.njit.edu/~bukiet/baseball/baseball.html
Using the performance data from all of the expected players, Bukiet applies a mathematical model to predict the final win-loss standings for every team in the league. Last year, Bukiet’s model correctly identified six of the eight playoff teams.
Unlike most predictors (my statistics friends would probably prefer I use the term projectors), Bukiet does not seem shy about comparing his past predictions to the actual results.
An interesting mathematical question would be “How can we measure how accurate these predictions really are?”
Application Appreciation
Rent Stability
As usual, I wasn’t thrilled when my landlord told me about this year’s rent increase. As someone familiar with how exponential growth works, I understand the power of the small, consistent percent increase.
After some mild protests, the landlord came back with some good news: he was going to reduce my increase by $25 per month! I wasn’t exactly thrilled with that, either, but it’s a gesture. And I thought to myself “At least I won’t be paying future increases on that $25!”
Which got me thinking: if my rent goes up 3% every year, how much of a difference will that $25 make? The answer: not much. In my lifetime, anyway.
At 3% per year, the $25 difference in rent now will be a $30 difference in 5 years. In 15 years, the difference in the two rents will be around $40. And if I stick around for 50 years, the difference will be about $90.
If I could stay here for 200 years, I’d see a big difference: almost $10,000! But then again, my rent would be around $1 million per month.
I’ll have to be content knowing that, while in the short term I don’t see much benefit, I win out as t goes to infinity.