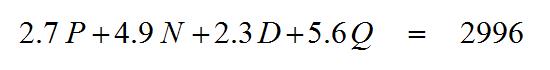patrick honner

Piggy Bank Estimations

Here are some interesting results regarding the recent Piggy Bank challenge.

Below are two graphs representing reader estimates. The graph on the left (Part 1) shows reader estimates without knoweldge of the weight of the Piggy Bank. The graph on the right (Part 2) shows reader estimates with knowledge of the weight.

The red bars represent the actual value of the Piggy Bank: $80.41. Not only are there significantly more “close” estimates in Part 2, the average estimate is $70.02; this is about 13% less than the actual value. Compare that with the average estimate in Part 1 of $46.98, which is about 41% less than the actual value.

Did readers actually use the knowledge of the weights to make a better “guesstimation”? Or is this perhaps an example of the anchoring effect?

Economics Sports

NBA Franchise Values

Every year, Forbes Magazine rates the value of all the franchises in the NBA. Here is the complete list:

http://www.forbes.com/lists/2011/32/basketball-valuations-11_rank.html

Surprisingly, the New York Knicks are now the most valuable team in basketball, topping the list at $655 million. Their 12% increase in value since last year certainly has something to do with the impact of Amar’e Stoudemire, who has raised both the team’s competitiveness and marketability. The fact that the Knicks carry no debt probably plays a part in their high valuation as well.

It appears as though the Knicks’ signing of Stoudemire last year to a 5-year, $100 million contract was a good move after all, despite my strong belief that it was a mistake.

It’s no surprise that LeBron James’ decision had serious financial ramifcations for both teams involved. The value of the Miami Heat rose 17% to $425 million. That’s an increase of nearly $60 million. The value of the Cleveland Cavaliers dropped 26% to $355 million, a decrease of nearly $130 million.

One might wonder where that extra $70 million in value went!

By patrick honner, 14 years8 years ago

Appreciation Photography

Math Photo: A Natural Discontinuity

And a jump-discontinuity, at that! I enjoy the jagged curves formed by cracking snow, where each turn is the product of some determinism and some randomness.

By patrick honner, 14 years8 years ago

Appreciation Technology

New Pi Record

A Japanese man has set a new world record by computing 5 trillion digits of pi.

http://www.reuters.com/article/idUSTRE70J7S220110120

Apparently Shigeru Kondo accomplished this feat using a home-built computer that worked non-stop for 90 days. Apart from this dramatic triumph for mathematical hobbyists (Kondo is a systems analyst for a food company), the article contains the following two excellent lines:

“Calculating a more accurate pi, which is believed to go on forever, has been a challenge for scholars for thousands of years.” Believed to go on forever? Is the reporter some kind of mathematical agnostic?

And this, from Kondo himself: “I really want to praise my computer, which calculated continuously for three months without complaint.” Credit where credit is due, I suppose.

It is interesting to note that, while 5 trillion is indeed the new record for consecutive digits of pi, researchers at Yahoo were able to compute digits that are much farther out than that; they just don’t know all the digits that lead up to it!

By patrick honner, 14 years8 years ago

Challenge

Coins in the Piggy Bank

Here’s the answer to the Piggy Bank Challenge!

Coinstar was nice enough to provide all the data I needed after it consumed my coins. As you can see, there was $80.41 in the Piggy Bank. The coinage consisted of 286 pennies, 92 nickels, 157 dimes, and 229 quarters.

Let’s take a quick look at some interesting strategies involving using the weight of the Piggy Bank to make an educated guess as to the total value. I’ve made some general remarks about reader guesses in a separate post.

As previously mentioned, the weight of the full Piggy Bank was about 2996 grams. Using the weights of individual coins, we can set up this linear equation:

where P, N, D, and Q are variables representing the number of pennies, nickels, dimes, and quarters, and each coefficient is the weight of that coin in grams.

This equation has several uses. First, you can try to establish some bounds for the value of the Piggy Bank by considering extreme cases. What if all the coins were quarters? What if they were all pennies? These cases would likely produce the maximum and minimum possible value of the Piggy Bank (is that obvious?).

Or, if you had some idea about how the coins were distributed, you could use this equation to estimate the total value of the Piggy Bank. One place to start might be assuming that there are equal numbers of each kind of coin. What other distributions might be used?

patrick honner

Math teacher in Brooklyn, New York

Application Challenge

Piggy Bank Estimations

Economics Sports

NBA Franchise Values

Appreciation Photography

Math Photo: A Natural Discontinuity

Appreciation Technology

New Pi Record

Challenge

Coins in the Piggy Bank

Follow Mr Honner