Map Estimation and Arclength

Whenever I spend a lot of time driving, navigating, and map-reading, I find myself making a lot of rough estimates of distances.  The process reminds me of how one estimates and ultimately evaluates, using Calculus, the arclength of a curve.

To find the length of a curve, we approximate the curve with a series of line segments.  It’s easy to find the length of a line segment, and so by sacrificing exactness, you turn a hard problem into an easy one.  This is a fundamental technique in Calculus.

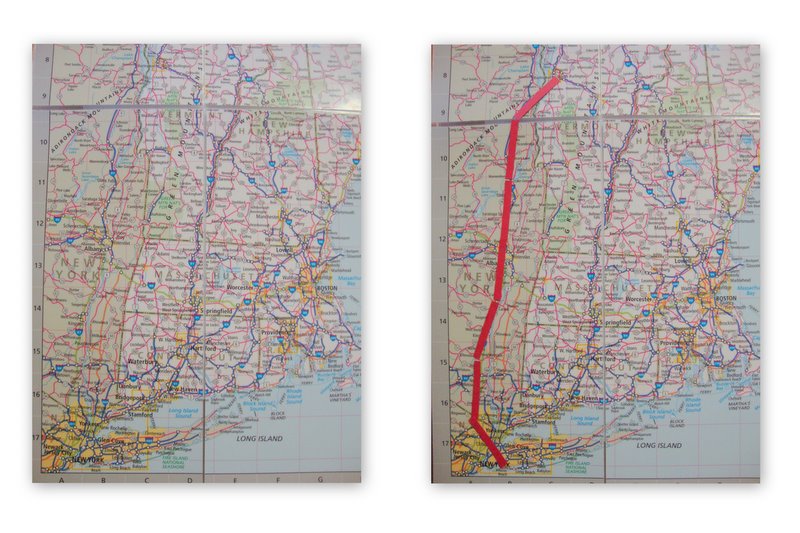
I made my line segments equal in length to 40 miles on the map.  Now just add up the lengths of the line segments to approximate the length of the curve.

Each of the seven line segments is (roughly) equal to 40 miles, so the approximate length of the path from Brooklyn to Burlington is 280 miles (not a terrible estimate).

There are plenty of ways to improve the approximation, and the straightforward, but complicated, calculus approach eventually produces the arclength integral.

On the actual drive my approximations weren’t as good, as I was using an inferior distance estimator.