Octomatics — The New New Math
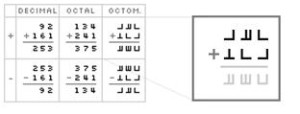It’s hard to tell how serious these people are about creating a new number system, but the effort is worthy of a little appreciation: introducing Octomatics!
Octomatics offers a new numeral systems that enjoys a visual addition method and a smaller multiplication table. They’ve also defined a new clock, a new calendar, and they’ve prototyped a new calculator!
Truth be told, I’ve always secretly desired a new clock and calendar system–one that wasn’t so archaic and contrived. I’m not getting my hopes up, though; Octomatics looks less like a paradigm shift and more like Esperanto to me.
10 Comments
Ahmed Gouda · October 15, 2010 at 5:59 pm
Just had an “epiphany”. As long as you make sure to carry the excess digits (Carry the ones), you can add, subtract,divide, or multiply pretty much any base. Although that base eight system would have definitely made the binary conversion test in digital electronics way easier. Though, even if that is true I doubt it’ll be easy to explain the concept to infants as easily as a base 10 system.
Roy D. Matheson · April 23, 2011 at 10:06 am
Dear Ahmed,
I think you will learn from experience that infants naturally understand octal-binary!
The idea that each column (in binary arithmetic)
has a value half or double of the neighboring column is such a simple idea…
What children have problems with is understanding why we use such a stupid, complicated math system…
Of course, many children are too wise to call us stupid…
Roy D. Matheson · April 23, 2011 at 10:22 am
I repent.
I apologize for using the word “stupid”.
Perhaps I should say “un-informed”.
Roy D. Matheson · April 23, 2011 at 10:39 am
Dear Ahmed,
It sounds like
you might be a genius
in math.
Please
ASK THE CREATOR
to teach you more…
HE (Blessed be HIS NAME)
IS FAR MORE INTELLIGENT
than we…
In octal-binary,
please consider the number
of days in a year.
Apparently,
the “nominal” dimension
is
365.2421875 days.
Please convert that to
octal:
555`174
and then look at it
in octal-binary.
I don’t know if this will post in three columns correctly:
1/128
1/16 1/32 1/64
1/8
———————
4 1
32 8
256 64
If you add up the above 11 values:
256 + 64 + 32 + 8 + 4 + 1 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128
it equals 555`174 (octal)
or in decimal
365.2421875
That is how THE CREATOR designed this planet:
365.2421875 days per year.
The internet rounds it off as 365.2422 days per year…
There is more…
Roy D. Matheson
(559) 432-4278 Fresno, California, USA
Roy D. Matheson · April 23, 2011 at 1:48 pm
I want to re-do the 555`174
1/128
1/16……1/32……1/64
………………………1/8
——————————
4……………………..1
32…………………….8
256……………………64
If only I could get the columns
to post as clean, straigh columns…
Roy D. Matheson · April 23, 2011 at 10:47 am
The above was taught to me
by Douglas Matheson
back around 1971.
Roy D. Matheson · April 23, 2011 at 11:48 am
I wish I knew how
to make the octal-binary
post correctly
in three columns,
so you can see the pattern:
Here is the basic pattern.
It extends to infinity
in both directions.
Please notice that it goes from right-to-left,
as in Arabic and…
Each value is twice as large
as the previous value.
In other words, these are 2^N power:
1,2,4,8,16,32,64,128,256…
I don’t know if this will post
in three neat columns.
I like to arrange them
in octal-binary
like this:
…
…
…
… (Please don’t forget! Right-to-left, like Arabic!)
…
1/128 1/256 1/512 = 8^(0-3)
1/16 1/32 1/64 = 8^(0-2)
1/2 1/4 1/8 = 8^(0-1)
—————————-
4 2 1 = 8^0
32 16 8 = 8^1
256 128 64 = 8^2
2k k k/2 = 8^3 Note: Here, k = 1,024 = 2^10.
16k 8k 4k = 8^4 “k” facilitates mental approximations.
128k 64k 32k = 8^5 (fast, in-your-head math)
k^2 (k^2)/2 256k = 8^6
8k^2 4k^2 2k^2 = 8^7
64k^2 32k^2 16,777,216 = 16k^2 = 8^8
512k^2 256k^2 128k^2 = 8^9
At this moment,
I see zero errors-of-fact
in the above
octal-binary
“basic chart”.
(signed) rm2
8:48 A.M. California time
Roy D. Matheson · April 23, 2011 at 11:49 am
Sorry!
The three columns
were “smashed” together
by somebody’s software…
Roy D. Matheson · April 23, 2011 at 1:42 pm
I guess I could have used dots
to separate the columns, like this:
1/16……1/32…..1/64 = 8^-2
1/2…….1/4……1/8 = 8^-1
..4………2…….1 = 8^0
.32……..16…….8 = 8^1
256…….128……64 = 8^2
Sorry I didn’t think of that sooner!
Roy D. Matheson · April 23, 2011 at 1:44 pm
I still wish
I could show that table
with neat, straight collumns.
If you can do spreadsheets,
you can quickly generate
your own (for the integers).