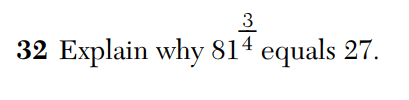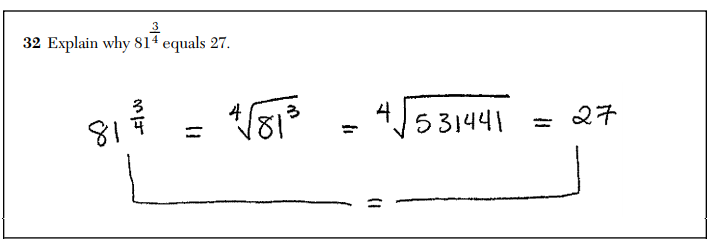This has quickly become my new least-favorite kind of Regents exam question. (This is number 32 from the January, 2018 Algebra 2 Regents exam.)

What can you say here, really? They’re equal because they’re the same number. Here’s a solid mathematical explanation. Right?

Wrong.

According to those who write the scoring guidelines for these exams, this is a justification, not an explanation. Because students were asked to explain, not justify, this earns only half credit.

This is absurd. First of all, this is a perfectly reasonable explanation of why these two numbers are equal. This logical string of equalities explains it all. This clear mathematical argument demonstrates what it means to raise something to the power 3/4.

Second, whatever it is that differentiates an “explanation” from a “justification” in the minds of Regents exams writers, it’s never been made clear to test-takers or the teachers who prepare them. A working theory among some teachers is that “explain” just means “use words”. Setting aside how ridiculous this is, if this is the standard to meet, students and teachers need to be aware of it. It needs to be clearly communicated in testing and curricular materials. It isn’t.

Third, take a look at what the the test-makers consider a “complete and correct response”.

In this full-credit response, the student demonstrates a shaky mathematical understanding of the situation (why are they using logarithms?) and writes a statement (“81 with four roots gives you 3”) that, while on the right track, is in need of substantial mathematical refinement. Declaring this to be a superior response to the valid mathematical argument above is an embarrassment.

These tests are at their worst when they encourage and propagate poor mathematical behavior. We deserve more from our high-stakes exams.

Related Posts

• Regents Recaps
• Is It Better to Justify or Explain?
• How Do You Explain that Two Things are Equal?
• Common Core Algebra, “Explain Your Answer”
• It’s True Because It’s True
• Modeling Data
• What Do They Want to Hear?

On question 32 of the January, 2018 Common Core Algebra 1 Regents exam, students were asked to explain why a quadratic whose graph is given might have a particular set of factors. Here are two sample student responses from the state-produced Model Response Set.

On the left, the student says “Yes”, sets each factor to 0 and solves, and produces the roots x = -2 and x = 3. On the right, the student says “Yes, because the x-intercepts are (-2,0) and (3,0).”

One of these responses received full credit, the other half credit. I posted this to Twitter and invited people to guess.

One of these responses got full credit, the other got half credit. Which is which?#math #mathchat pic.twitter.com/4fw1QK2GWP

— Patrick Honner (@MrHonner) February 11, 2018

According to the official scoring guide, the response on the right earned full credit: it is a “complete and correct response”. The response on the left earned half credit, because the student “gave a justification, not an explanation.”

It seemed as though the majority of respondents on Twitter favored the response on the left; a few even specifically said it offered a better “explanation” than the full-credit response. Many did choose the response on the right, especially those familiar with how New York’s Regents exams are scored.

To me, both answers are unsatisfying. The full-credit response offers an “explanation” but is devoid of justification: the student doesn’t make the connection between the x-intercepts and the roots. The half-credit response derives the roots algebraically, but fails to explicitly connect the roots to the intercepts. It’s hard for me to accept that one of these responses is substantially better than the other: both responses expect the reader to fill in an equally important gap.

It’s also hard for me to accept what counts as “explanation” here. Several teachers familiar with New York’s Regents exams commented that, in this context, “explain” simply means use words. And we’ve seen example after example of ridiculous “explanations” on these exams. It sends the wrong message to students and teachers about what constitutes mathematics, and since the message is transmitted via high-stakes exams, it can’t be ignored.

Related Posts

• Regents Recaps
• How Do You Explain That 2 + 3 = 5?
• How Do You Explain Two Things are Equal?
• Common Core Algebra, “Explain Your Answer”
• It’s True Because It’s True
• Modeling Data