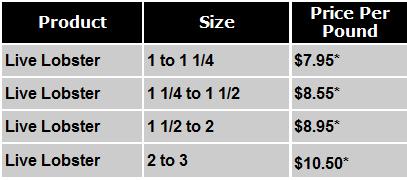
One of the benefits of travelling around New England is enjoying lobster in its many forms: steamed, on a roll, in a bisque, biting your toe. But while shopping at a fishmonger one evening, I was somewhat baffled to see a sign like the one at the right. It seems that the price per pound for lobster varies depending on the lobster’s size!
Why is this? Why should a larger lobster cost more per pound than a smaller lobster? Large or small, apples are still $1.69 per pound; the same goes for onions, chicken, and most other things.
What’s different about lobsters? My assumption is that, in a lobster, the ratio of meat to non-meat (shell, antennae, veins, etc) is constant, that is, the same for any size lobster. Thus, since you are paying for meat, you should then pay the same price per pound for any lobster. But maybe that’s not the case. Maybe in a small, one pound lobster, there is, say, 8 oz of meat and 8 oz of shell, but in a lobster twice the size, there is 20 oz of meat and 12 oz of shell.
I guess I assumed that the geometry of the lobster is essentially the same regardless of the size; in other words, that all lobsters are geometrically similar. Thus, the price-per-pound should be lobster-independent. But maybe I’m wrong. Is it really the case that, as lobster size increases, the amount of meat and the amount of non-meat increase at different rates?
Anyone have any other theories?
