Here is another installment in my series reviewing the NY State Regents exams in mathematics.
This is question 27 from the Geometry exam.
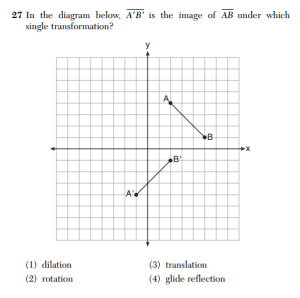This question has two correct answers: it is possible to map AB onto A’B’ using a glide reflection or a rotation. The original answer key indicated that (4) glide reflection was the correct answer. After the exam was administered, the state Department of Education issued a correction and told scorers to award full credit for both (2) and (4).
Mistakes happen, even on important exams that many people work hard to produce. But when mistakes are made, those responsible should accept responsibility, not equivocate.
Here’s the official correction from the state.
It’s hard to accept that the issue here was a lack of specificity in the wording of the question. The issue is that someone wrote a question without fully thinking through the mathematics, and then those tasked with checking the problem also failed to fully think through the mathematics. This isn’t a failure in communication; this is a failure in management and oversight.
And it has happened before. This example is particularly troubling, in which those responsible for producing these exams try to pretend that an egregious mathematical error is really just a lack of agreement about notation. Sometimes errors are just erased from the record with little or no explanation, and then, of course, there are the many mistakes that are never even acknowledged.
Mistakes are bound to happen. But by pretending that substantial errors are just misunderstandings, differences of opinion, or typos, the credibility of those responsible for these high-stakes exams suffers even further damage.
