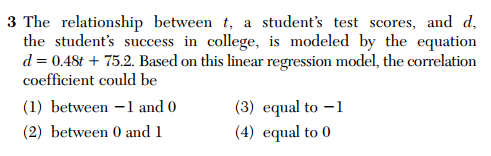February 2013

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

There seems to be some confusion among the Regents exam writers about when students are supposed to learn about lines and parabolas.  Consider number 39 from the January 2013 Integrated Algebra exam:

Compare the above problem with number 39 from the June 2012 Geometry exam:

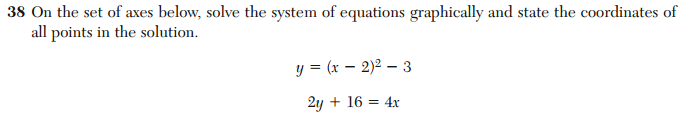These questions are essentially equivalent.  They both require solving a system of equations involving a linear function and a quadratic function by graphing.  Yet, they appear in the terminal exams of two different courses, that are supposed to assess two different years of learning.

When, exactly, is the student expected to learn how to do this?  If the answer is “In the Geometry course”,  the Algebra teacher can hardly be held accountable if the student doesn’t know how to solve this problem.  And if the answer is “In the Integrated Algebra course”, what does it mean if the student gets the problem wrong on the Geometry exam?  Is that the fault of the Geometry teacher or the Algebra teacher?  The duplication of this topic raises questions about the validity of using these tests to evaluate teachers.

And if that isn’t confusing enough, check out this problem from the 2011 Algebra 2 / Trig exam.

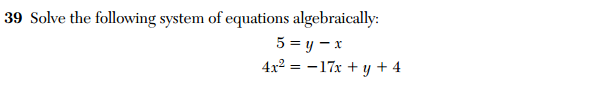Here, we see the same essential question, except now the student is required to solve this system algebraically.  These three exams–Integrated Algebra, Geometry, Algebra 2/Trig–span at least three years of high school mathematics.  In the integrated Algebra course, a student is expected to solve this problem by graphing.  Then, 2 to 3 years later, a student is expected to be able to solve the same kind of problem algebraically.

What does that say about these tests as measures of student growth?

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

One significant and negative consequence that standardized exams have on mathematics instruction is an over-emphasis on secondary, tertiary, or in some cases, irrelevant knowledge.  Here are some examples from the January 2013 Regents exams.

First, these two problems, number 10 from the Algebra 2 / Trig exam, and number 4 from the Geometry exam, emphasize notation and nomenclature over actual mathematical content knowledge

Rather than ask the student to solve a problem, the questions here ask the student to correctly name a tool that might be used in solving the problem.  It’s good to know the names of things, but that’s considerably less important than knowing how to use those things to solve problems.

The discriminant is a popular topic on the Algebra 2 / Trig exam:  here’s number 23 from January 2013:

It’s good for students to understand the discriminant, but the discriminant per se is not really that important.  What’s important is determining the nature of the roots of quadratic functions.

If you give the student an actual quadratic function, there are at least three different ways they could determine the nature of the roots.  But if you give them only the discriminant, they must remember exactly what the discriminant is and exactly what the rule says.  This forces students and teachers to think narrowly about mathematical problem solving.

In number 3 on the Algebra 2 / Trig exam, we see a common practice of testing superficial knowledge instead of real mathematical knowledge.

Ostensibly, this is a question about statistics and regression.  But a student here doesn’t have to know anything about what a regression line is, or what a correlation coefficient means; all the student has to know is “sign of the correlation coefficient is the sign of the coefficient of x”.  These kinds of questions don’t promote real mathematical learning; in fact, they reinforce a test-prep mentality in mathematics.

And lastly, it never ceases to amaze me how often we test students on their ability to convert angle measures to the archaic system of minutes and seconds.  Here’s number 35 from the Algebra 2 / Trig exam.

A student could correctly convert radians to degrees, express in appropriate decimal form, and only get one out of two points for this problem.  Is minute-second notation really worth testing, or knowing?

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

Consider the following problem from the January 2013 Algebra 2 / Trigonometry exam:

What’s interesting about this problem is what it doesn’t tell you.

The student here is expected to assume that the terms in the sequence keep going up by 9.  That is, the student is expected to assume that the sequence is arithmetic.  Once the student makes that assumption, they can use the appropriate formula to sum the first 20 terms.

Encouraging students to assume that arbitrary sequences are arithmetic is bad practice.  It can develop in students a sense that sequences are usually arithmetic, which will make it harder for them to understand non-arithmetic sequences later on.

More generally, we don’t want students getting into the habit of making unconscious assumptions about problems.  By forcing them to make assumptions that fit the problem to the test, questions like this train students not to ask questions like “Are we sure the next term is 50?  What else might it be?”.  This was one of the main points of my talk “g = 4, and Other Lies the Test Told Me“.

It’s not outrageous that think that this sequence might be arithmetic.  But the mathematical world is a rich and complex place.  Are we really sure that this sequence is arithmetic?  After all, maybe what we’re really looking at is the sequence of numbers whose digits add to five!

Am I thinking too deeply about this sequence?  Maybe.  But as a teacher, thinking deeply about mathematics is precisely what I want my students to do.