Regents Recap — January 2013: What Are We Testing?
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
One significant and negative consequence that standardized exams have on mathematics instruction is an over-emphasis on secondary, tertiary, or in some cases, irrelevant knowledge. Here are some examples from the January 2013 Regents exams.
First, these two problems, number 10 from the Algebra 2 / Trig exam, and number 4 from the Geometry exam, emphasize notation and nomenclature over actual mathematical content knowledge
Rather than ask the student to solve a problem, the questions here ask the student to correctly name a tool that might be used in solving the problem. It’s good to know the names of things, but that’s considerably less important than knowing how to use those things to solve problems.
The discriminant is a popular topic on the Algebra 2 / Trig exam: here’s number 23 from January 2013:
It’s good for students to understand the discriminant, but the discriminant per se is not really that important. What’s important is determining the nature of the roots of quadratic functions.
If you give the student an actual quadratic function, there are at least three different ways they could determine the nature of the roots. But if you give them only the discriminant, they must remember exactly what the discriminant is and exactly what the rule says. This forces students and teachers to think narrowly about mathematical problem solving.
In number 3 on the Algebra 2 / Trig exam, we see a common practice of testing superficial knowledge instead of real mathematical knowledge.
Ostensibly, this is a question about statistics and regression. But a student here doesn’t have to know anything about what a regression line is, or what a correlation coefficient means; all the student has to know is “sign of the correlation coefficient is the sign of the coefficient of x”. These kinds of questions don’t promote real mathematical learning; in fact, they reinforce a test-prep mentality in mathematics.
And lastly, it never ceases to amaze me how often we test students on their ability to convert angle measures to the archaic system of minutes and seconds. Here’s number 35 from the Algebra 2 / Trig exam.
A student could correctly convert radians to degrees, express in appropriate decimal form, and only get one out of two points for this problem. Is minute-second notation really worth testing, or knowing?


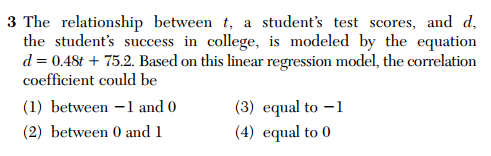
8 Comments
Graeme McRae · February 25, 2013 at 1:39 pm
In problem 10, a smart student can throw away answers (2) and (4) without even reading the question, since they are the same. This leaves a reasonable answer and an unreasonable one. So what is this testing? It’s testing the ability to do well on tests.
MrHonner · February 25, 2013 at 6:44 pm
There is no question “testing well” is a skill in and of itself. It’s just not clear the skill has much real value.
Alexis Farmer @destroyboy · February 25, 2013 at 3:04 pm
bloody hell. a recent question on my daughters oxford cambridge reading exam asked “write down a muliple of 12”. Stupid question because zero is a valid answer. But will the examiner know that?
MrHonner · February 25, 2013 at 6:43 pm
I’ve been involved in communal grading where teachers weren’t identifying legitimate problem-solving methodology that deviated from the rubric. Luckily we had a rigorous checking system in place, but I’m not sure all schools (or private companies) do.
Abe Mantell · February 27, 2013 at 9:26 am
I agree with the author, in principle, that the labels (names) we attach to procedures or even symbols
should not be the emphasis, but rather the mathematical thinking of problem solving.
However, certain terms and symbols are used in mathematics, as in any field, and I think it is
reasonable to expect students to remember terms like permutation, discriminant, correlation, etc.
…especially if they are emphasized in class, as I suspect is done in HS Regents classes (in addition
to spending 6-8 weeks of the year practicing old Regents exams which also emphasize such things).
As another example, shouldn’t we (as well as science and engineering faculty) expect students in
credit courses to know what is meant by “scientific notation” rather than have to explain (on an exam)
what is meant by it?
Plus, I am not sure, but I think the formula for nPr may even be given among the list of formulas on
the Regents exam.
MrHonner · February 28, 2013 at 11:11 am
Abe-
I, too, believe that proper notation and terminology are important in mathematics. I want students to understand how various notations represent our mathematical objects, and what our terms mean (and, as importantly, what they don’t mean).
But these are high-stakes, terminal exams. As such, they represent the core learning objectives of the course. I don’t think identifying correct notation should be a core learning objective, especially not at the expense of problem solving.
And since these exams influence a student’s graduation status, a teacher’s job, or a school’s existence, they become the de facto curriculum for these courses. As instruction bends to these tests, it bends toward that which is easy to test (notation, vocabulary, memorization of facts) and away from what’s really important in mathematics (process, problem-solving, context).
Bowen Kerins · April 10, 2013 at 12:14 am
The correlation coefficient is not what you described, it is a measure of the fit quality of the data. The correlation coefficient is not necessarily 0.48; it can be anything between 0 and 1. If all the data were exactly on the given line, the correlation coefficient would be 1. It must be positive because the fitting line has a positive slope.
This makes it an even worse question, since many students can answer it correctly without having a clue what they are doing. Indeed if you gave the exact same question with the equation d = 4.82t – 0.53, many students would pick choice (1) simply because they see a number between -1 and 0.
Never mind that neither t nor d is given in any reasonable sense of units. Oof. This question is horrible.
MrHonner · April 10, 2013 at 6:56 am
Thanks for pointing out the error, Bowen. What I meant to say was that if the student is merely taught the signs of a and r are the same, they can do this problem without knowing anything about what any of this means. I’ve made a correction.
And of course, this is exactly how this topic is taught, as I’m sure virtually no one teaches (or knows?) how to calculate a correlation coefficient by hand.
What’s amusing about your second point is that the exam writers themselves made the mistake of mixing up a and b on an earlier test: https://mrhonner.com/2012/01/29/regents-exam-recap-january-2012/.