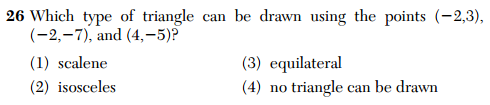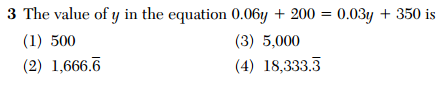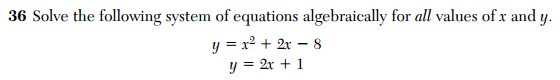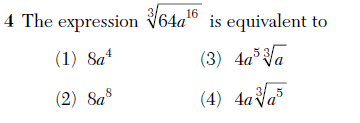Teaching

N Ways to Apply Algebra with the New York Times — Comments

I was very happy with how well my piece “N Ways to Apply Algebra with the New York Times” has been received.  Written for the New York Times Learning Network, this article was a response to this summer’s editorial “Is Algebra Necessary?”.  My intention was to create opportunities for teachers and students to see and use algebra in the context of New York Times content and resources.

The piece generated a lot of comments, some of which I found quite surprising.  For example,

This piece does an excellent job of demonstrating Mr. Hacker’s point – that algebra is unnecessary for most of daily life and work. Each of the above exercises is merely a more tedious and academic way of finding information that is readily available via the web or a simple calculator  (link)

Naturally I disagree that the exercises are “tedious” and “academic”, but what really surprises me is the claim that if some piece of information is readily available via the web or calculator, then there’s no reason to teach it.

The commenter specifically refers to an activity which explores how various formulas govern housing prices, interest rates, and mortgage payments.  While it is true that technologies exist that can calculate mortgage payments for us, students need more than just awareness of the existence of these formulas.  House payments, car payments–debt payments in general–play a significant role in modern life.  Students should explore the mathematics of these situations and develop experience, intuition, and understanding about the implications of that mathematics.

The above commenter agreed with an earlier comment:

These examples are pretty awful. No one would ever calculate mortgage payments using the actual formula. No one.   (link)

Even if you believe no one would use the actual formula, how do calculators and computer programs find the answers for us?  By using the actual formula.

I don’t like the suggestion here that it’s ok to tell students something like “It’s not important for you to know how mortgage payments are calculated; it’s good enough for you to know that someone else can do it for you.”  This is wrong, both as a teaching matter (our goal should be to empower students) and as practical matter (are banks and mortgage lenders always trustworthy?).

Lastly, I found this comment both shocking and saddening:

I’m getting a PhD in Math Education. … I think the article pretty much proves that Algebra is not necessary. I am still, after many years, hoping to talk to someone other than an engineer who can give me an example of using Algebra in the workplace. As for using it in real life, I have never heard of it happening and I do not see it happening here.  (link)

Someone earning a PhD in Math Education has no idea how anyone other than engineers use algebra in their jobs.  And they proudly state that they have never heard of algebra being used in “real life”.

This is a purported expert in mathematics education, someone who, presumably, will be teaching and training future math teachers.  And what will this person tell those future math teachers?  That algebra isn’t necessary.

By MrHonner, ago

Math Lesson: N Ways to Apply Algebra with the New York Times

My latest contribution to the New York Times Learning Network is a math lesson written in response to the editorial “Is Algebra Necessary?”, and contains a number of algebraic activities that can be explored using New York Times content and resources.

N Ways to Apply Algebra with the New York Times

Teachers and students can mathematically model mortgages, car costs, election predictions, and much more!

Algebra may not be necessary, but it sure is useful!

By MrHonner, ago

Regents Exam Recap: August 2012

Here is a brief review of the August 2012 New York State Math Regents exams, as part of my on-going series examining the quality and validity of these tests.

Only the Integrated Algebra and Geometry exams were offered in August 2012, presumably due to financial constraints.  Here are a few thoughts regarding some selected questions from those tests.

First, some issues that are probably minor to most, but important to me as a mathematician and a teacher.  Here is number 26 on the Geometry exam.

What does it mean to “use” a point in drawing a triangle?  Obviously, the author meant that the given points were to be the vertices of the triangle, but why not say that?  Technically, I could use a point by drawing a line segment through it; as such, I could draw any kind of triangle using the given points.

Number 3 on the Integrated Algebra exam includes a particular pet peeve of mine.

There is no value of y in the given equation.  In fact, that’s the entire point of a variable:  it can take any value!  What the author means is “What value of y makes the following equation true?” , so why isn’t that the question?  In addition to asking a question that actually has a correct answer, this would also model for students the correct way to think about variables and equations.

Here’s another problem from the Integrated Algebra exam, number 36:

There’s nothing mathematically wrong with this particular question.  However, the Integrated Algebra exam is the first of the high school mathematics exams in New York City.  It is meant to be taken after an introductory algebra course, which means that most students will take this test in 9th or 10th grade.

Thus, it is strange to note that this question, on the 9th grade exam, is virtually the same as the highest-valued question on last year’s Algebra 2 / Trigonometry exam.  The Algebra 2 / Trig exam is highest level math exam in the state.   It is usually taken in 11th or 12th grade.

So where should this question be?  Is it part of the 9th-grade curriculum?  Or the 11th-grade curriculum?  The authors of these exams seem a bit confused about this.

In addition, the August 2012 Geometry exam contained one of the most embarrassing math Regents questions I’ve ever seen, but I’ll address that in a separate post.

By MrHonner, ago

Regents Recap — June 2012: Some Improvement

Here is another installment from my review of the June 2012 New York State Math Regents exams.

I tend to be rather critical in my evaluation of these exams, pointing out poorly constructed, poorly phrased, and mathematically erroneous questions.  However, there have been some minor improvements of late.

First, it seems as though, in general, the wording of questions has improved slightly.  To me, questions on the June 2012 exams were more direct, specific, and clear than in the recent past.

There were also some specific mathematical improvements.  For example, although graphs were often unscaled, they seemed generally more precise, avoiding issues like this asymptote error.

There were considerably fewer instance of non-equivalent expressions being considered equivalent.  The problem below avoids the domain-issues that plagued recent exams.

Perhaps it’s just luck, but we’ll give the exam writers the benefit of the doubt for now.

And the Algebra 2 / Trig exam definitely demonstrated a more sophisticated understanding of 1-1 and inverse functions, which is good to see in the wake of this absolute embarrassment from last year.

Perhaps someone has been reading my recaps?

Let’s hope we see continued improvement in the clarity and precision of these exams.  If these exams are going to be play such an important role in today’s educational environment, it seems of utmost importance that they be accurate and well-constructed.

By patrick honner, ago
Follow

Get every new post delivered to your Inbox

Join other followers: