Resources

How Can Infinitely Many Primes Be Infinitely Far Apart — Quanta Magazine

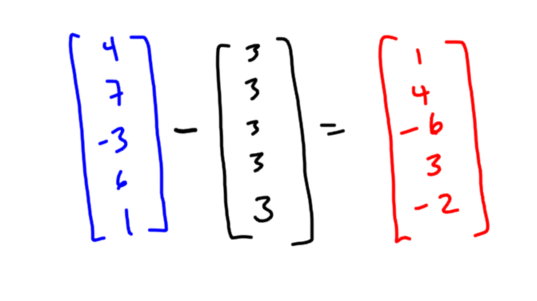
My latest column for Quanta Magazine ties recent news about “digitally delicate” primes to some simple but fascinating results about prime numbers.

You may have noticed that mathematicians are obsessed with prime numbers. What draws them in? Maybe it’s the fact that prime numbers embody some of math’s most fundamental structures and mysteries. The primes map out the universe of multiplication by allowing us to classify and categorize every number with a unique factorization. But even though humans have been playing with primes since the dawn of multiplication, we still aren’t exactly sure where primes will pop up, how spread out they are, or how close they must be. As far as we know, prime numbers follow no simple pattern.

There’s a tension among the infinitude of prime numbers — that there will always be primes close together and primes far apart — that can also be seen among digitally delicate primes, primes that become composite if any digit is changed. It may come as a surprise that any digitally delicate primes exist at all, but that’s just the beginning of their story. Find out more at by reading the full article here, and be sure to check out the exercises!

By MrHonner, ago

Why Claude Shannon Would Have Been Great at Wordle — Quanta Magazine

My latest column for Quanta Magazine uses the viral word game Wordle to explore the basic ideas of information theory, the branch of mathematics developed by Claude Shannon that revolutionized fields as diverse as digital communication and genetics.

Wordle is a perfect place to discuss the way Shannon defined “information” to posses certain important mathematical properties, like additivity and and inverse relationship with predictability.

For example, how would you proceed if your Wordle guess came back like this?

What you guess next says a lot about you both as a Wordle player and as an information theorist. To learn more, and maybe even level up your Wordle game, read the full article here.

By MrHonner, ago

Introducing Painless Statistics

I am thrilled to announce the release of my new book, Painless Statistics!

Painless Statistics, an entry in the Barron’s Painless series, is written to serve as both a supplementary resource for students taking statistics in school as well as a stand-alone resource for adults who are learning (or re-learning) stats on their own.

Painless Statistics begins with an example of working with data, and covers everything from summary statistics and representations of data to sampling distributions and statistical inference. The book also includes plenty of problems that get you thinking about and applying the important ideas in each chapter.

My hope is that Painless Statistics can be a useful resource for middle school, high school, and even college students learning statistics, as well as for lifelong learners interested in understanding the fundamental mathematical ideas at the intersection of statistics, probability, and inference.

I also think the book would be a great resource for any math teacher who might not see themselves as a statistics teacher but would like to better understand the fundamental ideas in statistics. If by reading Painless Statistics you learn 10% of what I learned by writing it, I think you’ll find it a worthwhile purchase.

If you or someone you know is learning statistics, or would like to learn statistics, please consider picking up a copy of Painless Statistics! It will be available in bookstores everywhere starting June 7th, and you can also order it online. I’ve included the Table of Contents below, and you can take a look inside at the first chapter here.

Painless Statistics Table of Contents

Chapter One: An Introduction to Data

Chapter Two: Data and Representations

Chapter Three: Descriptive Statistics

Chapter Four: Distributions of Data

Chapter Five: The Normal Distribution

Chapter Six: The Fundamentals of Probability

Chapter Seven: Conditional Probability

Chapter Eight: Statistical Sampling

Chapter Nine: Confidence Intervals

Chapter Ten: Statistical Significance

Chapter Eleven: Bivariate Statistics

Chapter Twelve: Statistical Literacy

By MrHonner, ago

What a Math Party Game Tells Us About Graph Theory — Quanta Magazine

My latest column for Quanta Magazine explores some deep (and recent!) results in graph theory using a simple mathematical party game. Trying to get your entire group of friends to each shake an odd number of hands leads to some fundamental and surprising results, like the impossibility of some simple configurations.

This also ties in to some recent research that has determined new bounds on the way a graph can be partitioned into subgraphs. You can read the full article here, which includes some fun and challenging exercises at the end.

By MrHonner, ago

The All 1s Vector

Here’s a short post based on a Twitter thread I wrote about a very underappreciated vector: The all 1s vector!

Image

Every vector whose components are all equal is a scalar multiple of the all 1’s vector. These vectors form a “subspace”, and the all 1’s vector is the “basis” vector.

Let’s say you have a list of data — like 4, 7, -3, 6, and 1 — and you put that data in a vector v. An important question turns out to be “What vector with equal components is most like my vector v?”

To answer that question you can *project* your vector onto the all 1’s vector. You can think of this geometrically — it’s kind of like the shadow your vector casts on the all 1’s vector. There’s also a formula for it that uses dot products.

Image

Because of the way the dot product works and the special nature of the all 1’s vector, v•a is the sum of the elements of v and a•a is the number of elements in v. This makes (v•a)/(a•a) the mean of the data in v!

Image

Since 3 is the mean of your data, the vector with equal components that is most like your vector is the all 3’s vector. This makes sense, since if you’re going to replace your list of data with a single number, you’d probably choose the mean.

Now the cool part. Look at the difference in these two vectors: These are the individual deviations from mean for each of your data points, in vector form!

Image

And geometrically this vector of deviations is perpendicular to the all 1’s vector! You can check this using the dot product.

Image

So data can be decomposed into two vector pieces: one parallel to the all 1’s vector with the mean in every component, and one perpendicular to that with all the deviations. You can see hints of independence, variation, standard deviation lurking in this decomposition.

You can check out the original thread on Twitter here, including some very interesting replies!

Related Posts

By MrHonner, ago
Follow

Get every new post delivered to your Inbox

Join other followers: