My latest piece for the New York Times Learning Network gets students investigating the mathematics of gerrymandering. Through applying geometry, proportionality, and the efficiency gap, students explore the notion of a “workable standard” for identifying and evaluating biased electoral maps.
Here is an excerpt:
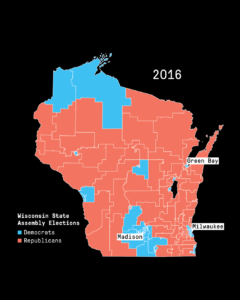
Math lies at the heart of gerrymandering, in which the shapes of voting districts and distributions of voters are manipulated to preserve and expand political power.
The strategy of gerrymandering is not new… However, new, sophisticated mathematical and computer mapping tools have made gerrymandering an even more powerful way to tilt the playing field. In many states, where the majority party has the authority to rewrite the electoral map, legislators essentially have the power to choose their voters — to create districts in any shape or size that will weaken their opponents and increase their dominance.
In this lesson, we help students uncover the mathematics behind these biased electoral maps. And, we help them apply their mathematical knowledge to identify and address the problem.
In fact, the questions students will work through are similar to those the Supreme Court is now considering on whether gerrymandering can ever be declared unconstitutional.
The article was co-authored with Michael Gonchar of the NYT Learning Network, and is freely available here.
Related Posts
