Geometry

Some Strange Circles

I was trying to construct a simple, introductory intersection problem for the first day of Calculus class, so I started with a well-behaved circle:

This is a circle centered at (3,2) with radius 5.  I picked two points on the circle, (0,6) and (7,-1), found the equation of the line between them, and put together my system of equations:

So I had successfully reverse-engineered my circle-and-line intersection problem with two nice solutions:  (0,6) and (7,-1).

Unfortunately, I made a typo on the handout.  At the end of the left side of the circle equation I wrote ” + 12″ instead of ” – 12″.

So all my work was for naught.  Or so I thought.  Turns out, at least two amazing things happen:

First, the new circle still ends up having a nice radius, namely 1.  What’s even more amazing is that the new circle also ends up having two nice intersections with the given line, (3,3) and (4,2)!

Strange Circles

I wish my intentional work always turned out as well as this mistake!

By patrick honner, ago

3-D Illusion Application

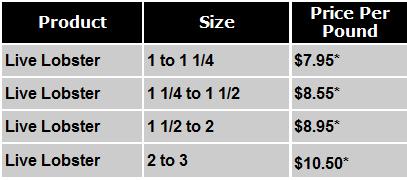
child in streetThis is a clever (and creepy) application of optical illusions–a painting, drawn on the pavement, that appears to on-coming drivers as a child playing in the middle of the street.

http://reviews.cnet.com/8301-13746_7-20016169-48.html

The purpose of this, presumably, is to catch the attention of drivers so that they will slow down.

The illusion is strikingly effective, and by watching the video you can see how long the image on the ground is.  I wonder if the painting is equally stretched out at all points–is it just a dilation of a normal drawing?–or is it more of a distorted projection–like Greenland on a flat map?  That is, is the head of the painting five-times normal size, while the shoes of the painting are twice normal size?  My gut feeling is that the painting needs to be distorted like that, but I’m not really sure.

Now, whether this strategy will prevent accidents or actually cause more accidents remains to be seen.

By patrick honner, ago

Lobster-nomics

lobster pricesOne of the benefits of travelling around New England is enjoying lobster in its many forms:  steamed, on a roll, in a bisque, biting your toe.  But while shopping at a fishmonger one evening, I was somewhat baffled to see a sign like the one at the right.  It seems that the price per pound for lobster varies depending on the lobster’s size!

Why is this?  Why should a larger lobster cost more per pound than a smaller lobster?  Large or small, apples are still $1.69 per pound; the same goes for onions, chicken, and most other things.

What’s different about lobsters?  My assumption is that, in a lobster, the ratio of meat to non-meat (shell, antennae, veins, etc) is constant, that is, the same for any size lobster.  Thus, since you are paying for meat, you should then pay the same price per pound for any lobster.  But maybe that’s not the case.  Maybe in a small, one pound lobster, there is, say, 8 oz of meat and 8 oz of shell, but in a lobster twice the size, there is 20 oz of meat and 12 oz of shell.

lobsters

I guess I assumed that the geometry of the lobster is essentially the same regardless of the size; in other words, that all lobsters are geometrically similar.  Thus, the price-per-pound should be lobster-independent.  But maybe I’m wrong.  Is it really the case that, as lobster size increases, the amount of meat and the amount of non-meat increase at different rates?

Anyone have any other theories?

By patrick honner, ago

Limits and Oar Making

A boat-builder once described to me one procedure for making oars.

real oar (2)Start with a long piece of lumber with a square cross-section.  Take off a certain amount from each of the four corners.  Now their are eight corners.  From each of the eight corners, take off a smaller amount.  The progression of cross-sections looks something like this:

oars

Through practice, the builder knows how much wood to remove at each stage.  You can continue to repeat this process, but some sanding at this point will probably get you pretty close to what you are looking for:  a circular cross-section.

This naturally brings to mind the hallmarks of Calculus:  approximations and limits.  At each stage of the process, the cross-section of the oar becomes a better and better approximation of a circle.  Indeed, the limit of such a process is indistinguishable from a circle.

I’m not sure if anyone making oars is thinking about Calculus, but sometimes it’s hard for me not to think about it!

By patrick honner, ago

More Math and Fruit (Vegetables?)

I was cutting up some squash the other day

squash 1

and I thought I’d experiment cutting the squash into fifths and sixths.

I thought I would do a much better job cutting the squash into equal sixths than into equal fifths.  I am generally more comfortable with even numbers, and there is something quite unnatural about cutting a circle into fifths.  But I’m not sure either division was especially equal.

cut squash
They both tasted great, though!

By patrick honner, ago
Follow

Get every new post delivered to your Inbox

Join other followers: