Geometry

Appreciation Geometry

12/5/13 — Happy Right Triangle Day!

Happy Right Triangle Day! Today we celebrate a favorite geometric object: the 5-12-13 right triangle.

Of course, the sides of this triangle satisfy

$5^2 + 12^2 = 13^2$

and, thus, form a right triangle. But one reason I like this particular right triangle so much is the role it plays in another favorite triangle. The 5-12-13 triangle fits together perfectly with the 9-12-15 right triangle

to make the 13-14-15 triangle!

The 13-14-15 triangle is special in its own right: it is a Heronian triangle, a triangle with rational side lengths and rational area. In fact, this triangle has integer side lengths and integer area, making it especially interesting!

Happy Right Triangle Day! If you’re in New York City, you might want to join the Museum of Math as they pythagorize the Flatiron Building!

By MrHonner, 11 years9 years ago

Appreciation Geometry Photography

Sunday Morning Tiling Problem

By MrHonner, 11 years11 years ago

Appreciation Geometry

Decomposing Functions into Even and Odd Parts

When it comes to functions, the concepts even and odd have always been important to me as a teacher. Connecting the algebraic and geometric representations of mathematical ideas is a primary goal in my classroom, and these concepts provide great opportunities to do that.

Algebraically, a function is even if 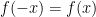$f(-x) = f(x)$ , and this condition manifests itself geometrically as symmetry with respect to the y-axis in the graph of 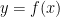$y = f(x)$ . A function is odd if 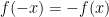$f(-x) = -f(x)$ , and geometrically this means that the graph of 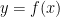$y = f(x)$ is symmteric with respect to the origin. Knowing a function is even or odd provides a wealth of information to work with, and can make solving some problems trivially easy.

But it wasn’t until recently that I learned the following amazing fact: Functions can essentially be uniquely decomposed into even and odd parts!

Claim: Let 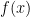$f(x)$ be a non-zero, real-valued function whose domain is symmetric about the origin; that is, 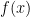$f(x)$ exists implies 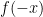$f(-x)$ exists. Then 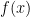$f(x)$ can be uniquely expressed as the sum of an even function and an odd function.

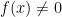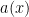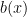Proof: For any function $f(x) \neq 0$ , define the functions $a(x)$ and $b(x)$ in the following way:

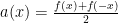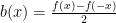
$a(x) = \frac{f(x)+f(-x)}{2}$ and $b(x) = \frac{f(x)-f(-x)}{2}$

First, we see that

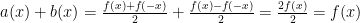$a(x) + b(x) = \frac{f(x)+f(-x)}{2} + \frac{f(x)-f(-x)}{2} = \frac{2f(x)}{2} = f(x)$ .

Next, since 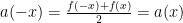$a(-x) = \frac{f(-x)+f(x)}{2} = a(x)$ , we have that 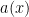$a(x)$ is even.

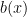Similarly, since $b(-x) = \frac{f(-x)-f(x)}{2} = -\frac{(f(x)-f(-x))}{2} = -b(x)$ , we have that $b(x)$ is odd. Thus, 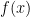$f(x)$ can be expressed as the sum of an even function and an odd function.

Now, suppose 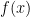$f(x)$ could written as the sum of an even and an odd function in two ways:

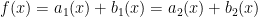
$f(x) = a_{1}(x) + b_{1}(x) = a_{2}(x) + b_{2}(x)$

A little algebra gives us

$a_{1}(x) - a_{2}(x) = b_{2}(x) - b_{1}(x)$

Since the sum of even functions is even and the sum of odd functions is odd, we have an even function, 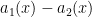$a_{1}(x) - a_{2}(x)$ , equal to an odd function, 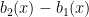$b_{2}(x) - b_{1}(x)$ . The only function that is both even and odd is the zero function (another fun proof!), therefore

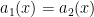
$a_{1}(x) - a_{2}(x) = b_{2}(x) - b_{1}(x) = 0$

and so

$a_{1}(x) = a_{2}(x)$

$b_{1}(x) = b_{2}(x)$

Thus, this representation of 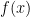$f(x)$ is unique. (Note: since 0 is both even and odd, we can consider 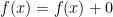$f(x) = f(x) + 0$ to be the unique decomposition in case 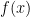$f(x)$ is itself even or odd.)

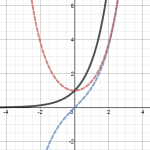
I was fortunate to encounter this unfamiliar fact at a time when hyperbolic trig functions were on my mind, which made it obvious to me where the hyperbolic sine and cosine functions come from: They are the even and odd parts of 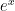$e^x$ !

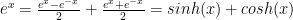
$e^x = \frac{e^{x} - e^{-x}}{2} + \frac{e^{x} + e^{-x}}{2} = sinh(x) + cosh(x)$

I also used this fact in a fun but inefficient proof that the derivative of an even function is an odd function.

Are there are other cool consequences of this unique decomposition of functions?

Related Posts

Derivatives of Even Functions

By MrHonner, 12 years4 years ago

Appreciation Geometry

5/12/13 — Happy Right Triangle Day!

Happy Right Triangle Day! Today we celebrate a favorite geometric object: the 5-12-13 right triangle.

Of course, the sides of this triangle satisfy the Pythagorean Theorem

$5^2 + 12^2 = 13^2$

but one reason I like this particular right triangle so much is the role it plays in another favorite triangle. The 5-12-13 triangle fits together perfectly with the 9-12-15 right triangle

to make the 13-14-15 triangle!

Happy Right Triangle Day! Be sure to marvel at some perpendicularity today.

By MrHonner, 12 years12 years ago

Appreciation Geometry

Spiral Shadows

Studying vector calculus tends to make you see space curves everywhere you go. Here’s a conical helix (or a helical cone?).

A good way to understand the behavior of curves in space is to understand how their projections behave. The sun does a nice job of showing us one such projection of this space curve.

This suggests a common mathematical practice: trading a hard problem for an easier one. Space curves can be difficult to analyze, but their projections are more easily understood. And by understanding its projections, you can develop knowledge of the space curve itself.

Of course, it’s important to understand what information you lose through the projection, as well!

By patrick honner, 12 years12 years ago

Follow Mr Honner