This bungee-swing at Coney Island is one of the tallest trapezoids I have ever seen. And isosceles, to boot!
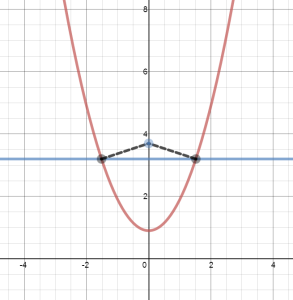 While playing around with distances from points to graphs, I discovered the following interesting property of parabolas.
While playing around with distances from points to graphs, I discovered the following interesting property of parabolas.
Suppose you have a standard parabola, , and a point on its axis of symmetry,
. Then the point on the graph of the parabola closest to the point
either has y-coordinate equal to
, or is the vertex of the parabola.
A calculus-based proof is fairly straightforward.
The distance between a point on the parabola, say and the point
is given by
To find the minimum distance, differentiate to get
This derivative is undefined when the denominator is zero, which only happens when the point is the vertex. The derivative is zero when
By the zero-product property, either or
.
The critical value corresponds to the vertex of the parabola. The distance from
to the vertex is a minimum if
, or a relative maximum when
.
Now, if , we have
. Since
on the parabola, the point associated with this critical value has y-coordiante
. Some simple analysis shows that the distance to this point is minimal.
As an alternative to optimization, one could approach the problem geometrically. Since the shortest path from a point to a line is the perpendicular line segment connecting them, the shortest path between a point and a curve should be a line segment perpendicular to a tangent to the curve. At a point on the parabola , the slope of the tangent line is
, and so the slope of the line perpendicular to the tangent at
would be
. This is equivalent to
, and since
is the distance to the axis of symmetry, it follows that this line intersects the axis of symmetry at a point a half-unit up in the y-direction.
This fun and surprising result would make a nice exploration in a Calculus class. It easily extends to general parabolas, and the situation naturally suggests some compelling extension questions.
You can explore the problem, and create variations, in this interactive Desmos demonstration I put together.