Solve for x!
Challenge Probability
Events with Probability Zero
I just donated this shirt to the Salvation Army. I estimate the probability that I will ever see this shirt again to be zero. In fact, forget estimating: I think the probability that I will see this shirt again is exactly zero.
In fact, I’ll go even further than that: I claim that the probability that anyone who reads this ever sees this shirt is exactly zero. Not .0000000000001. Zero.
Even if there are infinitely many possible scenarios in which this shirt is seen by someone, this number is dwarfed by the infinitude of possible scenarios in total. Thus
moderate infinity ÷ really big infinity = zero
I dropped it off at the Salvation Army in Brooklyn. Let me know if you see it: evidence will be required to claim your prize.
Application Challenge
Comprehensive Calorie Counting
There’s an interesting op-ed in the NYT about how mathematics is used to put food production and consumption into context:
http://www.nytimes.com/2010/08/20/opinion/20budiansky.html
For example, we can measure food transportation costs in calories (as a calorie is, indeed, a unit of energy), and so we can look at production and transportation costs of certain foods and compare them to the calorie content of the food itself. For example, it takes about 5000 calories to produce a 100-calorie head of lettuce.
The author’s intent is to poke holes in some of the common arguments used by proponents of “eating local”: Transportation costs for most foods are neglible compared to household storage and preparation costs, says the author, thus “eating local” is not an especially eco-friendly strategy. However, the author hilmself makes a number of weak and erroneous arguments, comparing “apples to rocks” in some cases.
The piece offers some interesting mathematical ideas and a good critical reading exercise.
Challenge Geometry
Problem-Solving Under Pressure
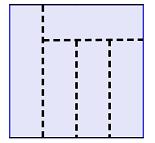
Near the end of a long morning building a small table, I encountered the following simple geometry problem: I needed to cut four small rectangles from a square of self-adhesive rubber to serve as the feet of the table’s legs. So I cut the square into four equal strips, lopped off the end of each
and had my feet.
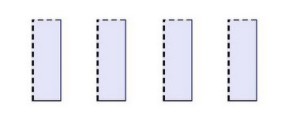
All well and good, but I missed the superior solution that any decent problem solver should have seen immediately:
This solution would have left me with one long rectangular remainder, as opposed to four small square remainders.
After working on the table for a while, I was mentally and physically drained, and I think this affected my ability to see the better solution. I guess it makes sense that being tired [and frustrated!] would negatively impact one’s ability to solve problems.
It’s interesting to think about how our physical, mental, and emotional states can affect our problem-solving abilities. And I think this suggests that problem-solving stamina is something we might want to work on.
Application Appreciation Challenge
Mathematics of Construction
One of the items on my to-do list was build something. To that end, I spent the afternoon turning a bunch of leftover lumber into a small table.
I’ve always admired those who can build elegant and functional things, but I came away from my project with an even greater appreciation for carpenters, woodworkers, builders, and the like. The measuring: how far are those legs spaced apart? The calculating: when all these pieces get put together, how tall is this thing supposed to be? The engineering: why are things rolling off my table? It’s a set of serious cerebral challenges on top of the obvious physical demands.
One theme that stood out as I slowly assembled my table was that of error propagation. A tiny error at an early stage (a millimeter or two of slant on a “flat” cut on a leg) can produce a sizable error in the end (things quickly rolling off your table).
It put me in mind of the classic differential problems in elementary calculus. For example, suppose you are measuring the diameter of sphere with a margin of error of +/- .1 mm: how much error might this generate in calculating the volume of the sphere? The surface area?
An even more complex problem is understanding how different errors interact with each other, which is something I experience frequently while putting this table together!