The tilling station is one of my favorite exhibits at the Museum of Mathematics. These rabbit tiles create a hexagonal tiling of the plane. Pick any rabbit, and you’ll notice six rabbits all around it; this is exactly how hexagons fit together to tile the plane.
What I really like about this tiling is the the various levels of triangles that emerge. Triangles of rabbits, one of each color, mutually intersect at ears and paws. And I can’t help but seeing the monochromatic rabbit triangles!
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
The Common Core standards have brought a slight increase in three dimensional reasoning into high school Geometry. I think this is generally a good thing: 3D geometry is typically given short shrift in this course, but is a beautiful and intriguing topic.
It can also be a confusing topic, as these problems from the inaugural Common Core Geometry Regents exam demonstrate.
According to the scoring guide, the correct answer is (4) a cone. Technically, however, the correct answer is (3) a right triangle.
Rotation is a rigid motion: it does not change a figure’s size or shape. If a right triangle is rotated about an axis, it will remain a right triangle. Presumably, the intent of this question is for the student to identify the solid of revolution formed by revolving the triangle about an axis. But that is a different question than the one posed. Ironically, the notion that rigid motions preserve size and shape is one of the fundamental principles in the transformation-based approach to geometry embodied by the Common Core standards.
Here’s another problematic 3D geometry question.
According to the answer key, the correct answer is (2). But the actual correct answer is all of these. While most cross-sections of spheres are circles, some cross-sections of spheres are single points (when the cross-sectional plane is tangent to the sphere). All the given objects have single point cross-sections as well, thus, could all have the same cross section as a sphere.
This is certainly not the first time we’ve seen problematic three dimensional geometry questions on these Regents exams (here’s a particularly embarrassing example), and I’ve been chronicling mathematically erroneous questions on these tests for years. Errors like this are often dismissed as insignificant, or “typos”, but because of the high-stakes nature of these exams, these errors have real consequences for students and teachers.
If these exams don’t model exemplary mathematics and mathematical practice, their credibility in evaluating the mathematical practice of students and teachers must be questioned.
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
One of the biggest differences between the new Common Core Regents exams and the old Regents exams in New York state are the conversion charts that turn raw scores into “scaled” scores.
The conversions for the new Common Core exams make it substantially more difficult for students to earn good scores. The changes are particularly noticeable at the high end, where the notion of “Mastery” on New York’s state exams has been dramatically redefined.
Below is a graph showing raw versus scaled scores for the 2015 Common Core Algebra Regents exam.
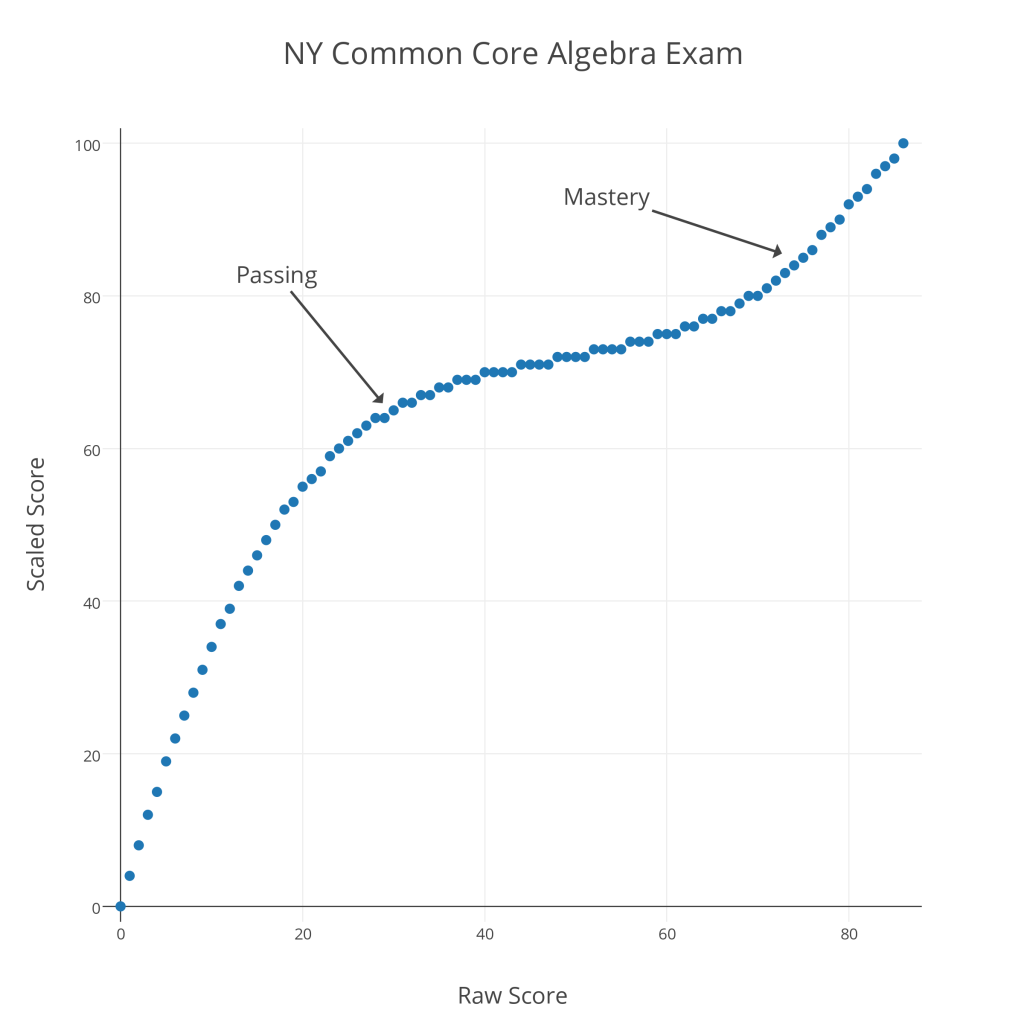As with last year’s Common Core Algebra Regents exam, there is a remarkable contrast between “Passing” and “Mastery” scores. To pass this exam (a 65 “scaled” score), a student must earn a raw score of 30 out of 86 (35%); to earn a “Mastery” score on this exam (an 85 “scaled” score), a student must earn a raw score of 75 out of 86 (87%). It seems clear that the new conversions are designed to reduce the number of “Mastery” scores on these exams.
Another curious feature of this conversion chart is what happens at the upper end. Consider the graph below, which shows the CC Algebra raw vs. scaled score in blue and a straight-percentage conversion (87% correct “scales” to an 87, for example) in orange.
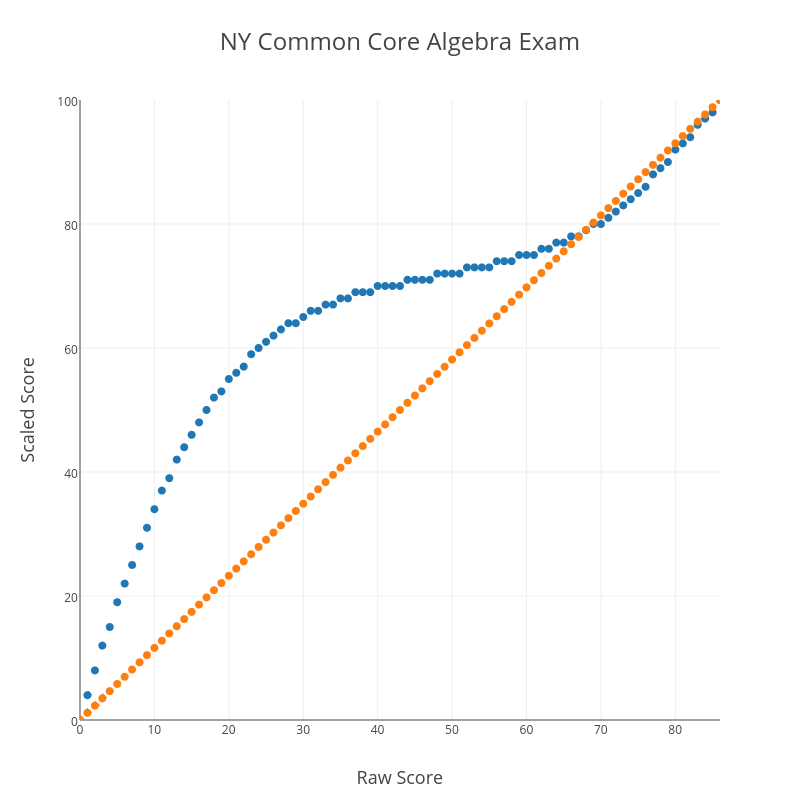
At the very high end, the blue conversion curve dips below the orange straight-percentage curve. This means that, above a certain threshold, there is a negative curve for this exam! For example, a student with a raw score of 82 has earned 95% of the available points, but actually receives a scaled score of less than 95 (a 94, in this case). I suspect there are people who will claim expertise in these matters and argue that this makes sense for some reason, but it certainly doesn’t make common sense.
One final curiosity about this conversion. It’s no accident that the blue plot of raw vs. scaled scores looks like a cubic function.
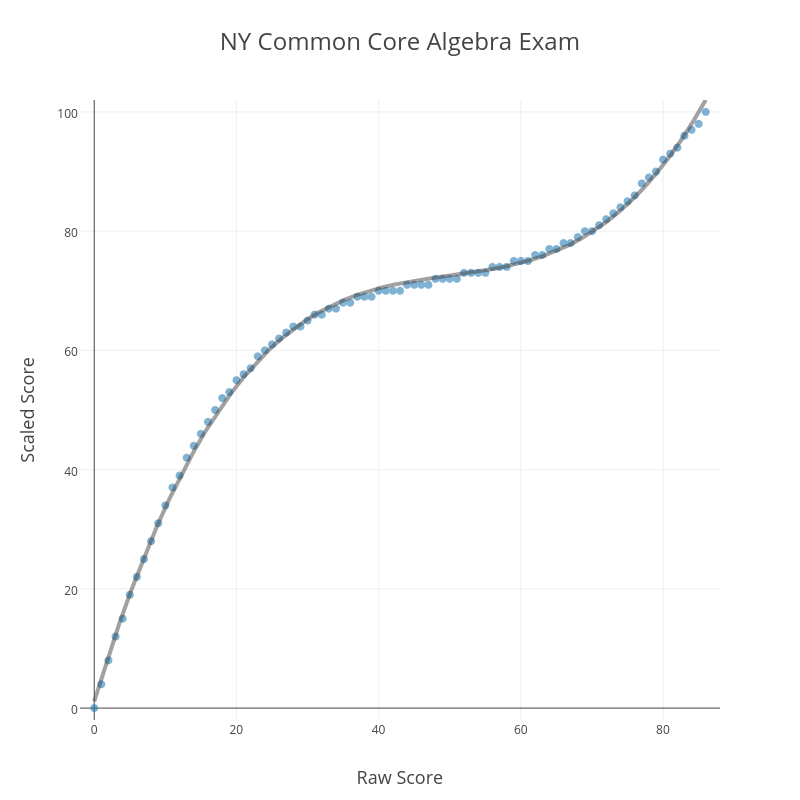
Running a cubic regression on the (raw score, scaled score) pairs yields
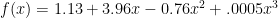
That is a remarkably strong correlation. Clearly, those responsible for creating this conversion began with the assumption that the conversion should be modeled by a cubic function. What is the justification for such an assumption? It’s hard to believe this is anything but an arbitrary choice, made to produce the kinds of outcomes the testers know they want to see before the test is even administered.
These conversion charts are just one of many subtle ways these tests and their results can be manipulated. Jonathan Halabi has detailed the recent history of such manipulations in a series of posts at his blog. These are the kinds of things we should keep in mind when tests are described as objective measures of student learning.
Related Posts
I am excited to once again be participating in the Bridges Math and Art conference this summer!
The Bridges organization has been hosting this international conference highlighting the connections between art, mathematics, and computer science since 1994.
I have participated in several Bridges conferences, and my experiences there have greatly influenced me as a mathematician and a teacher.
This year, I’ll be presenting a short paper, “Monte Carlo Art Using Scratch“, chairing a short paper session, and exhibiting a photograph in the Bridges Mathematical Art Gallery.
You can view the Bridges 2015 program here, see the entire 2015 Art Exhibit here, and learn more about the conference and the Bridges organization here.
Related Posts
I am proud and excited to be named a recipient of the Presidential Award for Excellence in Mathematics and Science Teaching!
The Presidential Award is the highest honor presented by the federal government for K-12 mathematics and science teaching. The awards are administered by the National Science Foundation on behalf of the White House and the Office of Science and Technology Policy. A rigorous application process begins at the state level, and state finalists are evaluated by scientists and educators at the national level.
This is a tremendous individual honor, but it is also a testament to the collaboration and support of many wonderful colleagues across schools and professional organizations who continually help me grow and evolve as a teacher. And to the students who challenge me every day to better challenge them. And most importantly, to the unending support I receive at home, from my family.
Recipients of the Presidential Award gather in Washington, D.C. for a series of celebratory and professional events. I’m looking forward to meeting a lot of inspiring teachers, and perhaps, the President!
The White House press release announcing the winners can be found here, and my PAEMST profile can be found here.
