This small section of rock wall conveys the challenge of arranging a collection of various shapes in an efficient, organized, way.
Resources
Proofs Without Words
This is a great collection of favorite Proofs Without Words from the community at MathOverflow.net:
http://mathoverflow.net/questions/8846/proofs-without-words
MathOverflow is geared toward research-level mathematics, so many of the examples deal with very advanced ideas. However, there are some lovely and accessible proofs of the sum of the first n squares, the sum of the first n cubes, the AM-GM inequality, and various Fibonacci identities.
And since it’s MathOverflow, the comments include a healthy debate about whether you can actually prove something with only a diagram!
Appreciation Geometry
11/11/11 — Equilateral Triangle Day!
While others celebrate the number 11 on this special day, I prefer to honor the Equilateral Triangle.
Last year, on 10/10/10, I celebrated the symmetry of the equilateral triangle. This year, I offer a favorite Proof Without Words. Well, a proof with some words. In any event, we will use equilateral triangles to prove that the following infinite series
is 
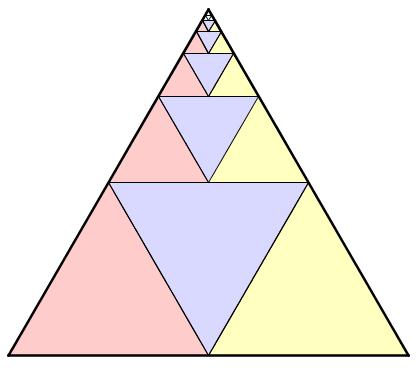
Consider the following diagram.
Notice that the largest blue equilateral triangle is
So, the sum of the blue triangles is
Let’s call this S.
Now, here’s the magic: the sum of the red triangles is also S! This is true because for every blue triangle, there is a congruent red triangle right next to it. Similarly, the sum of the yellow triangle is also S.
When you put all the blue, red, and yellow triangles together, you get the original triangle, whose area is 1. Thus, 3S = 1, and so
Therefore, we have
Happy Equilateral Triangle Day!
Related Posts
Geometry Teaching
The 11-10-11 Triangle
Today’s date, 11-10-11, reminded me to re-visit a recent post that posed the question “Which triangle is more equilateral: the 10-10-11 triangle, or the 10-11-11 triangle?”
The original post elicited lots of great comments from readers, who weighed in on what they thought the question meant and how they might go about trying to answer it. I offered one approach, and an answer to the question, in this follow up post.
As a math teacher, there are many reasons I try to create problems like this. Here are a few that I think are important.
First and foremost, in order to address this question, a significant amount of thought must be put into deciding what the question means. This process involves analysis, synthesis, reflection, and ideally discussion, all of which will be substantially mathematical in nature.
A second, related, virtue is that there is no obviously correct interpretation of what this question means. Mathematics is often viewed in stark terms: answers are either right or wrong. But the certitude of mathematics comes only after we agree on mathematical models for our given problem. There is often great debate about what those models should look like; the history of mathematics is full of such debate.
Problems like this one invite students into the modelling process, where they can discuss and debate the validity of various approaches. Moreover, the problem allows solvers to create multiple different models to explore, compare, and contrast. And in the end, we can pose and explore meta-mathematical question like “Which model most closely aligns with our intuitions?” and “Which model is the most useful?”
Lastly, this problem demonstrates one role creativity plays in mathematics. A simple response to the question, one I heard many times, is “Neither of these triangles are equilateral. They are both equally unequilateral.” Given our rigid definition of what equilateralmeans, this response is technically correct. But by relaxing our ideas about equilateral, by allowing ourselves to ponder what the phrase “more equilateral” might mean, by thinking creatively about what kinds of questions we can ask, we create an opportunity to explore, and possibly uncover, some new mathematical ideas.
History Resources
Biographies of Female Mathematicians
This is another nice resource provided by the School of Math and Statistics at the University of St. Andrews, Scotland: a collection of biographies of female mathematicians.
http://www-history.mcs.st-and.ac.uk/Indexes/Women.html
There are around 150 mathematicians profiled here. Each profile consists of a biography, a list of references, and links to other internet resources on the individual.
Among those profiled here are Maria Agnesi (of the Witch of Agnesi cubic curve), Emmy Noether (of Noetherian Ring fame), and Mary Ellen Rudin (topologist, and wife of Walter Rudin, a noted figure in Real Analysis).
A general collection of biographies is also available, as well as a fun-to-browse library of curves.