Through Math for America, I am part of an on-going collaboration with the New York Times Learning Network. My latest contribution, a Test Yourself quiz-question, can be found here:
https://learning.blogs.nytimes.com/2011/12/14/test-yourself-math-dec-14-2011/
This problem is related to the record low yields of acorns this year in the Northeast United States.
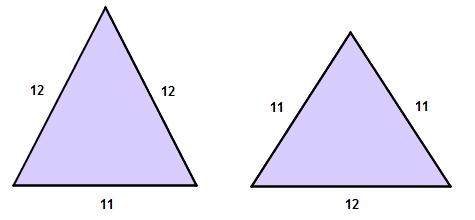
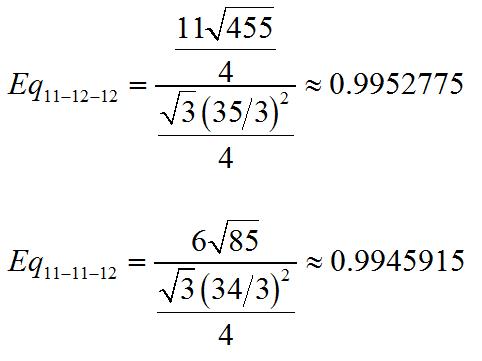Here’s an easy-to-understand, remarkably rich question that arose during a recent Math for America “Bring Your Own Math” workshop.
If a quadrilateral has a pair of opposite, congruent sides and a pair of opposite, congruent angles, is it a parallelogram?
I had a lot of fun thinking about this problem on my own, discussing it with colleagues, and sharing it with students. At different times throughout the process, I felt strongly about incompatible answers to the question. For me, that is a characteristic of a good problem.
I encourage you to play around with this. I was surprised at how many cool ideas came out as I worked my way through this problem, and I look forward to sharing them!
And if you want to see a solution, click here.
The passing of consecutive isosceles triangle days has me once again thinking about the question “Which Triangle is More Equilateral?”
I first considered the question on 10/10/11, comparing the 10-10-11 triangle and the 10-11-11 triangle. After a spirited discussion, I offered one approach to the question here. The problem gave me lots to think about, both mathematically and pedagogically, and I reflected on what I liked about this problem here.
But as 12/11/11 and 12/12/11 pass, I thought I’d revisit my strategy for answering the question “Which triangle is more equilateral?”
My basic strategy, outlined in more detail here, is to ultimately to quantify the circleness of each triangle. To me, being equilateral is all about trying to be as much like a circle as possible. So I created a measure to determine how close to circlehood a triangle is. Here are the numbers.
The 11-12-12 triangle’s measure is closer to 1, thus making it the more equilateral triangle.
Related Posts
When I see this star shape, I see it as two equilateral triangles meeting at a 60 degree angle. So it’s sort of a hexagon.
It’s been a fun few months for calendar math. Today is another Permutation Day: the month and day can be rearranged to form the year!
It certainly isn’t as exciting as the recent palindrome day, but it does make writing the date a little more fun!