Regents Recap — June 2012: Poorly Constructed Questions
Here is another installment from my review of the June 2012 New York State Math Regents exams.
Below are a few examples of what I consider “bad” questions. “Bad” here might mean poorly worded, poorly conceived, or irrelevant. In addition, there is an example of a question with a problematic rubric.
First, a type of problem that occurs regularly, one that is a pet peeve of mine. From the Algebra 2 / Trig exam:
The concept of “middle term” is artificial and depends entirely on how one chooses to evaluate the given expression. This question does not test an authentic mathematical skill; it tests how well a student executes one particular method of evaluating this particular expression.
Next, an example of a poorly-phrased question, one that confuses mathematical terminology. From the Integrated Algebra exam:
To “solve” a system of equations, one must find the ordered pairs that satisfy the given equations. Apparently this question wants only the y-values of those solutions, but the phrasing confuses what it means to “solve a system” and to “solve an equation”.
Students can probably figure out what the question-writer wants to hear in this case, but the lack of precision will only exacerbate confusion about the word “solve”.
Here’s a problem on the Algebra 2 / Trig exam that is simply irrelevant.
This question tests one thing, and one thing only: knowledge of an arcane and largely irrelevant notation, namely, degree-minute-second representation of angles. Would anyone outside the nautical or astronomical worlds consider this even remotely valuable?
Lastly, this question from the Integrated Algebra exam is formulated in a reasonable way, but the official scoring guide poses some unnecessary problems.
This question asks the student to graph an equation and then, using the graph, determine and state the roots of the equation. The correct answer is “2 and -4”, and with appropriate work, is worth three points.
However, if the student gives the answer “(2,0) and (-4,0)”, the student can only earn two out of the three points. So if the student gives the coordinates of the points where the graph crosses the x-axis, rather than names the “roots” of the equation, there is a one-third deduction.
While I believe that the distinction between roots and points is important, losing one-third credit seems seems unnecessarily punitive here. If we want to test student’s knowledge of vocabulary, there are better ways to do it than by sneaking it in at the end of an involved algebra problem.
Moreover, since the question requires that the student use the graph, the student is already being forced to interpret the problem in a geometric context. Penalizing them for thinking of the roots geometrically, then, doesn’t quite seem fair.
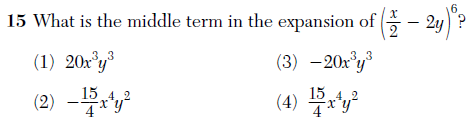
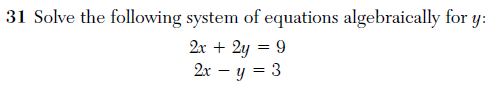
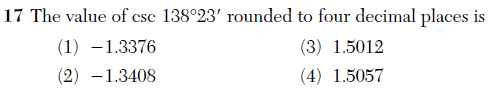
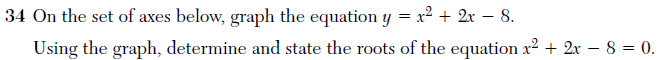
4 Comments
Marshall · August 10, 2012 at 11:06 am
I really appreciate posts like this. Very fun to read.
—
Regarding #31 above, in a way the concept of an ordered pair answer is a little removed from the question. It’s an arbitrary convention that we list the solution as the ordered pair (x,y) – a bit like the “middle term” concept. If it’s not x and y it can be unclear which one goes first. The default is alphabetical I suppose, or in context (independent var, dependent var).
I suppose my point here is that if a solution to a system is defined as the set of values of the variables that satisfy both equations at the same time, then (1) it doesn’t have to be listed as an ordered pair (and in a way that representation adds a layer of unnecessary context) and (2) as you say it makes absolutely no sense to ask for just one value at a time since it’s validity depend upon the other value(s).
—
Regarding #17, I would love it if someone could give me a legitimate reason to teach that seemingly archaic notation but thus far no one has been able to. Do people even IN nautical/astronomical still use minutes and seconds as convention?
MrHonner · August 10, 2012 at 11:26 am
Marhsall-
I see your point about ordered-pair notation being arbitrary. If pressed, I’d probably argue that ordered-pair notation is about as standard as convention gets in mathematics, but that’s not really the point here (no pun intended!).
For me, the issue in that particular problem is the on-going abuse of the word “solve”. It’s already terribly overloaded in math; it drives me crazy when kids say they are going to ‘solve’ (4 + 14) / 3, for example, and it’s frustrating to see official publications (exams in this case) muddying the waters even further.
bombastic · August 11, 2012 at 11:07 pm
I have heard complaints of this exam, but didn’t realize how bad it actually is. Not only does it focus on minutia, but by my count 8 of 27 MC questions are either equations that can be solved by plugging in the choices or expressions that can be compared by simply plugging in values for the variables. Do they realize the calculator has an “i” key (#28 give n in “simplest” form: i^13 + i^18 + i^31 + n = 0)? The wording on #27 is atrocious.
MrHonner · August 12, 2012 at 7:46 am
And this is the hardest of the NYS math exams. I’m not even sure why it’s called a “Trigonometry” exam at this point; the important ideas in that subject haven’t appear on the test in years.
The Integrated Algebra exam is even worse in this regard–answer half of the 30 multiple choice questions correctly and you pass.
All three exams have gotten progressively easier over the past 10 years (maybe longer), presumably to boost test scores and graduation numbers in pursuit of the education reform “miracle”.