The Perils of Teacher Blogging
I find my blog to be a very useful teaching tool. It’s full of resources for students to explore, and after doing so they often follow up in class with interesting questions and comments. The blog helps extend our mathematical conversations beyond the classroom. Sometimes, it works too well.
In a recent discussion on probability, we considered the following question:
Suppose you randomly choose a positive integer. What is the probability that the number you choose is divisible by five?
The students thought about the question and discussed their ideas. I asked for their thoughts. The usual good answers came out (
“The answer is zero,” he said. “Although there are infinitely many multiples of five and infinitely many total integers, the probability is zero because a small infinity divided by a big infinity is zero.”
“A small infinity divided by a big infinity is zero?” I responded, trying to appear as perplexed as possible. “That sounds kind of crazy to me. What does that even mean?” I tried to stir up the anti-zero sentiment in the room.
The student persisted. “According to you, a small infinity divided by a big infinity is zero.”
“That doesn’t sound like something I’d say,” I said, which is what I say when students remember something I wish they hadn’t. I usually get away with it. Not this time.
“You didn’t say it,” replied the student. “You wrote it on your blog.”
In a rare moment, I had no response. What could I say? I did write it on my blog. I had nowhere to hide.
The class celebrated this clear and decisive victory.
13 Comments
Jack "Epic Fail" H · May 26, 2011 at 9:19 am
Say it in roses, say it in mink, whatever you do, don’t say it in ink.
MrHonner · May 26, 2011 at 12:18 pm
Your advice, though poetic, seems at odds with the nature of blogging.
Thomas · May 27, 2011 at 10:58 am
I understand (at least I think I understand) how you can divide a smaller infinity by a bigger infinity, and how this would result in 0. However, I was pretty sure that finding a number divisible by 5 is not 0, or rather not impossible. I went to a random number generator and set the bounds as large as possible and generated a few numbers. It did not take more several tries to get a number divisible by 5, multiple times. Did I achieve the impossible several times? Or is it because I can’t set the limits to infinity so I can’t accurately test this out? Just curious.
JBL · May 27, 2011 at 9:37 pm
Thomas, the problem is that the terminology “smaller infinity” and “larger infinity” is very vague. In fact, we should probably think of “the integers” and “the multiples of 5” as having the same order of infinity; this is true in the sense of cardinality (they’re both countable sets) but more relevantly it’s true in the sense of density: a positive fraction of the first n positive integers is divisible by 5 as n gets very large. (In particular, this fraction approaches 1/5, and so the density of the multiples of 5 in the integers is 1/5.) This notion of density corresponds closely to what we mean by probability of choosing a random integer — in particular, it matches exactly what you were simulating with your experiment.
(Technical aside: it’s not really correct to talk about randomly choosing an integer, as there is no uniform probability measure on the integers, or on any countably infinite set. The notion of density is a good substitute, though.)
MrHonner · May 28, 2011 at 9:28 am
Thomas, here are two things to consider:
1) Part of your thought-process seems to be equating “probability = zero” with “impossible”. In some contexts this is true, but funny things happen when infinity gets involved!
2) You seem surprised, in part, because your empirical evidence contradicts the student’s argument. Are you sure the student’s answer was, in fact, correct?
MrHonner · May 28, 2011 at 9:31 am
Very cool stuff on density, Joel–that’s a nice way to think about it.
And you’re right, too, that the idea of “selecting an integer at random” isn’t as well-defined as people might think. James Tanton has a great video about how exploiting this vague notion of selecting things “at random” can be used to prove 1/3 = 1/2 !
Check out the video here: http://www.youtube.com/watch?v=uI2FnUmBeeo
JBL · May 28, 2011 at 7:13 pm
Cool, thanks for sharing the video — it’s a very nice presentation. I think I saw this problem once as a high school student (maybe at the CCNY summer program?) but that no one gave me a clear explanation at the time of how to resolve it (or at least, not an explanation I understood).
A few more words about density: in addition to asking what the density of a set is, we can also ask how quickly the limit converges. For example, we can show that the difference between the fraction of numbers less than
that are divisible by 5 and the limiting value 1/5 of this ratio is never more than and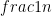 
, say. For the perfect squares, the density is 0, and the error is never more than 
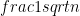. For the prime numbers, the density is 0, and the Prime Number Theorem tells us that the error is approximately 
(and how good this approximation is depends on whether or not the Riemann Hypothesis is true). Not every subset of the integers has a density, though — for example, try to compute the density of the numbers whose first (i.e., most significant) digit is 1.
John Paul Jones · May 28, 2011 at 9:57 pm
I like this post very, very much.
Thomas · May 29, 2011 at 3:37 am
Thanks for explaining, and for the video too. Also, I wasn’t sure the student was right, in fact I believed it was wrong from reading it first. The problem was it was it appeared to be a sound idea at first, just like how in the video it “proved” 1/2 = 1/3 when that obviously sounds wrong. I figured there was some sort of reconciliation, but couldn’t figure it out on my own.
I know this is about blogging but one last question out of curiosity. How come 1 is a “usual good answer” for the probability question? How did that student defend his or her answer? or are you just saying that was a usual answer?
MrHonner · May 29, 2011 at 12:43 pm
Finding that reconciliation is the challenging (and fun!) part, whether you’re working by yourself, or with others, to understand something. There is a lot of fun to be had in thinking about ideas that appear sound at first but lead to strange conclusions.
As far as the original question goes, the answer “1” comes up because someone might see this as “infinity / infinity”, which reduces to one. I consider it a “good” answer because there is some merit to the argument and it seems to conflict with our natural interpretations of probability (namely, probability = 1 is the same as “guaranteed”). So it’s a good place to have an interesting mathematical discussion.
Joel David Hamkins · March 19, 2016 at 10:31 am
I find this post confusing, because the infinity of the integer multiples of five is not actually a “smaller infinity” than the infinity of the integers. These two infinities have the same size, because the sets are put into one-to-one correspondence by the map that associates every integer n with the integer 5n.
But as others have mentioned, the way out is to talk about the density of the sets, rather than size of infinity. And the density of these sets are both finite numbers. The asymptotic density of a set A of natural numbers is the limit of the size of (A intersect {0,1,…,n} divided by n+1, if this limit exists. So the multiples of 5 have density 1/5, since as one goes higher and higher in the integers, the proportion of numbers that are multiples of 5 becomes as close as you like to 1/5.
This kind of talk about density also allows you to make sense of the idea of picking a number “at random”. (That concept does not make sense prima facie, since there is no uniform probability measure on the integers.) Rather, the question is really like this: suppose N is a large integers, and we randomly pick a natural number n<N. What are the odds that n is a multiple of 5. Well, for some small numbers, like N=7, the odds won't be exactly 1/5, and then when we go from N=9 to N=10, the odds will take a little jump, up to 3/11 (since 1,5,10 are, out of 11 numbers: 0,1,2,…,10). Then it will gradually decay 3/12, 3/13,… until it takes another little jump at N=15, up to 4/16. The asymptotic effect that one should notice is that as N gets larger and larger, the jump up counts for less and less, and the odds get closer and closer to 1/5. For most values of N, the odds are strictly greater than 1/5, and every five numbers have the odds exactly at 1/5.
MrHonner · March 19, 2016 at 12:51 pm
I appreciate the thoughtful reply from an infinity professional!
The students were celebrating the fact that I had been beaten at my own game and had no good reply, not the correctness of the student’s answer. We quickly resolved the matter of the probability being 1/5. Sorry if that wasn’t clear.
The small infinity / big infinity discussion came up in this post, where I imagined the space of all possible occurrences of seeing a discarded shirt to be dwarfed by the space of all possible occurrences. Something like (or much, much worse!) than picking an integer from the set of reals.
Joel David Hamkins · March 19, 2016 at 7:52 pm
That seems to resolve my confusion, thanks!
It must be great for the students in your class.