Regents Recap, January 2020: What is an Irrational Number?
This type of problem frequently appears on New York State Algebra 1 Regents exam.
There’s really no way for an Algebra 1 student to properly “explain” their answer to this question. Proving that a number is irrational is a concept from elementary number theory and is not part of the Algebra 1 course. What the test makers expect is for the student to simply state that a rational number times an irrational number is irrational. Not only is this not an explanation, but such a question reinforces the idea, for both students and teachers, that mathematics is a collection of facts to be memorized and regurgitated.
I’ve written about this issue before, but I didn’t think this kind of problem could get much worse. I was wrong. Here’s an example of a full credit response from the official scoring materials for the 2020 Algebra 1 Regents exam.
In this exemplar full credit response, the student erroneously represents 
The student has demonstrated some understanding of the situation, but doesn’t grasp the fundamental issue of what an irrational number is. This response shouldn’t get full credit. More importantly, the official scoring guidelines should not communicate erroneous mathematics to those who use them. How many teachers will walk away thinking this is valid? And then teach their students that to show a number is irrational, all you have to do is plug it into your calculator and see if it has eight digits past the decimal point?
This is kind of work that makes this other exemplar full credit response seem not so bad by comparison.
A lively Twitter thread on this problem can be found here.
Related Posts
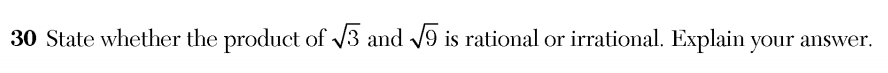
0 Comments