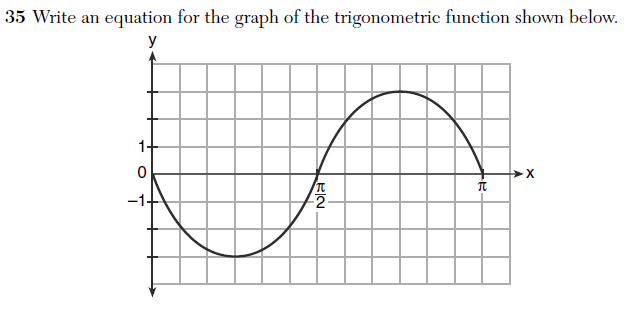
This is Not a Trig Function
I spend a lot of time looking at New York State Math Regents Exams. In addition to the critical analysis of the exams I undertake here, we typically grade several thousand exams at the end of each year at my school.
When grading so many exams, it’s not uncommon to feel disoriented and unsettled looking at the same problems over and over again. However, there was something particularly unsettling about this question.
This trigonometric function just appeared to be too round to me. Perhaps my senses were just dulled after hours of grading.
Thankfully, we have Geogebra to settle such mathematical disputes.
I was right! It is too round. Thanks again, Geogebra, for enabling my mathematical compulsions.
Related Posts
- Regents Recaps
- This is Still Not a Trig Function
- This is Not an Exponential Function
- These are Not Parabolas
- Still Not a Trig Function
42 Comments
Ihor charischak · October 24, 2012 at 9:34 am
What’s really amazing for me is that the test authors don’t use dynamic geometry software to produce their examples for print.
MrHonner · October 24, 2012 at 11:31 am
It amazes me, too. Is it just a lack of familiarity with the available technology?
John Sharp · October 24, 2012 at 9:35 am
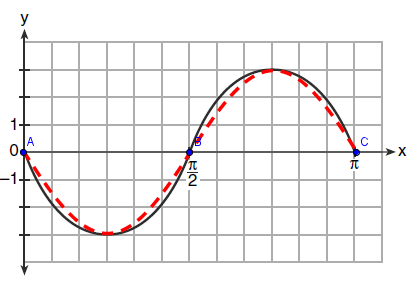
I thought the curve looked like an ellipse
If you go to Geogebra and put 5 points on the curve and then draw an conic through those 5 points, then you will see that is the case.
I would send you a file or a picture, but there is no way to communicate this through contacting you. I might be able to do that through twitter, but I don’t join any anti-social network sites
MrHonner · October 24, 2012 at 11:34 am
John-
You could always post a response on your blog and link to it.
Each half of the curve might be a “cap” of an ellipse (less than half, though). Of course, anything that looks like the cap of an ellipse also probably looks like some part of a parabola, too.
And I’m sorry to hear that you refuse to join any anti-social network sites. You are really missing out on a lot of anti-social interaction!
Sue VanHattum · October 24, 2012 at 9:48 am
Exactly what I was going to say. How did they produce that? It’s not two half-circles. That would have a vertical tangent at the middle. Here’s our challenge – what is that shape?!
MrHonner · October 24, 2012 at 11:35 am
Good challenge question, Sue! Geogebra would probably be helpful in generating a parametric model. I look forward to your answer. 🙂
Matthew N. Petersen · November 3, 2012 at 5:13 pm
That’s easy. It’s the sum of trig functions. 😛
MrHonner · November 3, 2012 at 7:13 pm
That’s a safe bet!
Tao Wang · October 24, 2012 at 3:57 pm
My off-the-top-of-my-head guess would be that each portion is a cubic Bezier curve. Perhaps what you get when you delegate math diagrams to typesetters using Adobe Illustrator or something similar?
John Sharp · October 24, 2012 at 4:30 pm
Try the ellipse method I outlined above in Geogebra. The curve is a perfect fit.
As you say, Tao, a typesetter would approximate a curve and it looks like they used two ellipses. Most would take the easy way out this way and not used sophisticated ideas like Bezier curves.
I am interested in the way people look at objects as well. Some people seem to be shape blind and could not see the difference between th ellipse and the intended sine wave. It is good to see everyone here can.
I do lots of research on anamorphic art (see my description at http://anamorphicart.wordpress.com/)
If you choose the “Plane anamorphosis” section and scroll down, you will see the painting of Edward VI by William Scrots which has two ellipses forming a band. Looked at from the correct point they resolve into circles. All books which show the resolved image by photography do not have circles.
In my experience, art historians seem particularly bad at being able to see and find perspective. It is very important to teach geometry not just for the mathematics, but to educate students in being able to see shape properly.
MrHonner · October 24, 2012 at 10:20 pm
John-
I’ve never really thought about “shape blindness”–it’s an interesting idea. I look forward to learning more about it, and about your research on anamorphic art.
One point I was trying to make earlier is that by playing around with parameters, I’m pretty sure I could “fit” a parabola to that piece of curve. Or an ellipse. Or maybe even some altered sine function. I’m not sure I believe that curve is any one thing. I’m not sure what that means for “shape blindness”.
Tao Wang · October 24, 2012 at 10:56 pm
I know that _we_ think an ellipse is a simpler idea than a Bezier curve, but many mass market CAD programs will use Bezier curves automatically since they are somewhat easy to understand for the end user — the control points are shown and all you have to do is click and drag them to get the curve you want.
I believe you that an ellipse fits the curve well. I’m just not sure that the guy typesetting this exam is thinking along those lines. If he or she has a program that can typeset an ellipse, one would assume that the program can typeset a sine function as well. Who knows??
MrHonner · October 24, 2012 at 10:13 pm
Never would have thought of that, Tao. Interesting insight.
David Patterson · October 25, 2012 at 8:07 am
Good find. Since no one seemed to post just what function it was, I took that as a challenge. 🙂
I used just a regular Google search and trial and error to figure out the function. It looks to me it is y=-3*sin(2x).
I guess if I was asked this question 20 years ago I might have been able to figure it out the way it was intended. 🙂
Henry Segerman · October 25, 2012 at 8:19 pm
It could have been made with Bezier curves, see
http://www.segerman.org/temp/Regents-2012-This-is-not-a-trig-function_with_beziers.png
The green curve is a Bezier curve I put on top of the image in Adobe Illustrator, so it fits. However, it’s also possible to do a much better approximation to a sine curve using Beziers (the blue curve).
MrHonner · October 25, 2012 at 9:49 pm
You win the award for going the extra mile, Henry. Thanks!
Tao Wang · October 26, 2012 at 12:56 pm
Ah! I did have the idea to put my hypothesis to the test. Just needed the motivation — I don’t have Adobe Illustrator, so I hacked up something JavaScript:
http://mathlaoshi.com/wp-content/uploads/2012/10/Bezier-Curve.html
Just click and drag.
MrHonner · October 26, 2012 at 6:30 pm
Very cool! Easy to see a “perfect” fit.
Andy Huynh · October 31, 2012 at 2:25 am
It’s generated by ellipses. To show how fast I can do it, I opened hte image in Photoshop and see how fast I can use the Ellipse tool to trace half of it. It only took me around two minutes. You guys are talking about Bezier curves as if you can’t generate ellipses with them, but how do programs like Photoshop and Illustrator generate ellipses? Bezier curves. When I use the Ellipse tool in Photoshop, it is creating a bezier curve. If a program gives you the option to create a bezier curve, there will probably be presets like rectangle, ellipses, polygons(though I never ran into a sine wave preset). And so I honestly don’t believe that the person who created this incorrect sine wave ended up using a curve tool and coincidentally matching a part of an ellipse. That person probably used the ellipse tool and some editing. So technically speaking, its probably a bezier curve imitating an ellipse.
Joshua Bowman (@Thalesdisciple) · November 1, 2012 at 8:45 am
The longer I look at that curve claiming to be a sine wave, the more distressing it becomes. We’ve been doing second derivatives and inflection points in calculus lately. Not only is the curve too round, there’s this awful sense that the second derivative is discontinuous.
MrHonner · November 1, 2012 at 10:25 am
Interesting point. We’re about to talk about the second derivative in my class as well–I hadn’t thought about this as an example, but it’s a great one. Thanks!
Sue VanHattum · November 1, 2012 at 12:54 pm
Is the first derivative discontinuous too? I had thought so, but now I’m not sure. How can you tell from a picture (of a continuous curve) that the 2nd derivative is discontinuous?
MrHonner · November 1, 2012 at 1:58 pm
I think the first derivative here is continuous, based on the apparent continuous transition of the tangent lines.
As for the second derivative, I guess the argument was that it “jumps” from concave up to concave down from one piece to the other without ever having concavity zero.
But now that you’ve made me really think about it, I suppose the second derivative here could be continuous, especially given the (presumed) symmetry of the curve.
Thanks for giving me something else interesting to think about, Sue!
Joshua Bowman (@Thalesdisciple) · November 4, 2012 at 8:15 pm
The symmetry of the picture does force the first derivative to be continuous, but not the second. To tell whether the second derivative is continuous, I imagine driving along the curve as a winding road. The second derivative measures how the steering wheel is turned (i.e., the change in direction, since the direction you’re pointed is what the first derivative measures). If the second derivative is continuous, then you can always turn the wheel smoothly as you go along the drive. If the second derivative is discontinuous, then at some point you have to jerk the wheel to a new direction.
For example, imagine a road made up of two circular arcs, meeting at a point in such a way that their tangent lines are aligned, but from that point they curve in opposite directions. When you’re driving along one arc, you have the wheel turned at a constant angle, because the curvature of the circle is constant. But when you reach the point where the two arcs are joined, you have to suddenly change the angle of the wheel so that you don’t fly off the road, even if the arcs are symmetric around the point where they meet. So second derivatives play a role in designing turns that can be navigated comfortably and safely.
With this figure, it looks to me like I would have to jerk the wheel if I were driving along a road shaped like this. That’s the awful sense I was trying to describe.
MrHonner · November 4, 2012 at 8:46 pm
As I see it, each “hump” is symmetric about its peak, and the two humps are congruent. They are put together in such a way that the entire diagram is symmetric with respect to the middle x-intercept.
I think this is sufficient information to conclude that the second derivative is continuous.
Sue VanHattum · November 4, 2012 at 9:03 pm
It seems like Joshua’s circular arcs would fit your description, and would, as he said, have constant acceleration – in some sense, though not a constant y”(x). Hmm, how would we calculate acceleration so that it would be a constant?
I’m convinced that the first derivative must be continuous and the second (if it’s circular arcs) discontinuous. This is continuing to be intriguing…
Joshua Bowman (@Thalesdisciple) · November 4, 2012 at 9:04 pm
Actually, that’s why I gave the example with the circular arcs—to show that the symmetry isn’t enough to guarantee continuity of the second derivative. However, I invoked curvature rather than the second derivative directly, so perhaps it’s simpler to consider parabolic arcs (I know, it’s been determined that the above example is composed of ellipses, but the principle is the same and easier to explain with parabolas).
A parabola is the graph of a quadratic function, whose second derivative is constant. You could take two congruent pieces of parabolas and glue them together with their tangent lines aligned (say, x^2+2x from -2 to 0 and 2x-x^2 from 0 to 2). The resulting graph corresponds to a function whose first derivative is continuous, but whose second derivative is piecewise constant—in my example it jumps from 2 to -2 at x=0.
Alexis Farmer @destroyboy · November 1, 2012 at 12:55 pm
A quadratic bezier curve is a rotated ellipse, they are the exactly the same shape/equation. I know this as I’m a low level graphics programmer and write routines to draw beziers a lot.
MrHonner · November 1, 2012 at 1:03 pm
Interestingly, Wikipedia says that quadratic Bezier curves are parabolic:
http://en.wikipedia.org/wiki/B%C3%A9zier_curve#Quadratic_B.C3.A9zier_curves
However, looking at the definition of the parametric curve given in the entry, I’m not sure I believe that x or y can be expressed as a quadratic function of the other coordinate.
Alexis Farmer @destroyboy · November 1, 2012 at 1:47 pm
I’m being stupid! I recently implemented some ellipse drawing routines and have them on the brain. They turned out to be tricky. A parabola can be spit down into smaller parabolas and that makes them easy to manipulate. I couldn’t figure out how to split the ellipse segment into smaller segments.
If the graph really is made of ellipses I think its most likely that the curve primitive used was actually an ellipse segment and not a bezier. It seems unlikely that whoever drew the graph would have gone to the trouble of approximating an ellipse with multiple bezier segments otherwise he could have tried to approximate a sine wave!
mr bombastic · November 5, 2012 at 7:55 pm
I don’t think it is quadratic either. Each section of the graph has 3 points that appear to be on corners of the grid. The parabola that “fits” those 3 points will not fit the rest of that section of the graph.
MrHonner · November 5, 2012 at 8:10 pm
If I could use small enough numbers in Geogebra, I’m pretty sure I could show you a parabola that looked like a good fit.
mr bombastic · November 10, 2012 at 5:21 pm
I am pretty sure you could not. I just dumped a larger version of the image into geobebra and remain convinced that there just isn’t enough “play” to fit a quadratic. Here is the goegebra applet: http://www.geogebratube.org/student/m21619
MrHonner · November 10, 2012 at 6:24 pm
I see the merit in your argument. I did something similar in Geogebra myself, with similar results. The issue is that you made the image only slightly bigger, by some small scale factor.
I feel that if I had another 2 or 3 decimals places to work with I could make it match. I think this is equivalent to a difference in scale of 100 to 1000.
In any event, I haven’t given up! Yet.
mr bombastic · November 11, 2012 at 12:03 am
The actual scale is not important – yes? y = f(x) & y = 1/1000 * f(1000x)have exactly the same shape other than one being blow up by a factor of 1000.
Are you just having an issue with the slider not being sensitive enough to changes in the parameters? I found that making the min & max values on the slider close together and the increment small allows for quite a bit of control. Making the slider segment longer adds more sensitivity as well.
Also, think of fitting the quadratic in the form: y = a(x-b)^2 + c. If you choose b & c so the vertex match, that only leaves a to play with – and it just isn’t that great of a fit – the parabola is clearly thinner than the “sine” wave. So you try and cheat a little by dropping the vertex of the parabola below that of the “sine” wave. But, by the time the part that is away from the vertex is matching a little better, it is obvious that the vertices don’t match.
In any event, thank you for posing an interesting problem. I believe I actually have a better understanding of parabolas after thinking about all this.
Alexis Farmer @destroyboy · November 1, 2012 at 12:58 pm
An ellipse is the same shape/equation as a quadratic bezier (the type with one control point) so my guess is that it is an ellipse and it was generated by a simple curve primitive in a drawing package. I know this as I’m a low level graphics programmer and have implemented beziers many times.
Ralf Muschall · November 3, 2012 at 1:28 pm
The curve looks wrong for me as well. At the second glance, I used the grid and saw that the curve essentially claims that sin(30°)=2/3 which is clearly wrong (sin(30°)=1/2).
Rocky Roer · November 17, 2012 at 10:13 am
I noticed this too. I wonder if i would have had the guts to realize the test was wrong, or if i would have struggled to find some trig question that did fit the graph. Would i have just answered with a sine curve which they were going for, or assumed it was a really hard question involving transformations, or sine squareds, or what not. And would my students have noticed? How would they respond?
MrHonner · November 17, 2012 at 11:53 am
Unfortunately, I think tests like these too often teach students not to notice these sorts of things. Which is a shame, because figuring out what’s wrong with this “trig” graph is a great mathematical activity.
Radu Grigore · November 3, 2012 at 1:53 pm
There’s a very easy way to see that the graph is wrong without using any software: sin(pi/12) = 1/2, and in the picture it clearly is 2/3.
MrHonner · November 3, 2012 at 2:05 pm
You have to be a bit careful as this isn’t y = sin(x) but some transformation of sine, but yes, you can use some basic trig values to see that the proportions are definitely incorrect!
MrHonner · November 4, 2012 at 9:56 pm
Sue and Joshua-
Unfortunately I can no longer reply directly to the above thread, but thanks for following up–I now see exactly what you are talking about. The explicit parabola example made it very clear (I just actually worked it out myself and then saw your comment, Joshua!).
If you haven’t already seen it, Timothy Gowers noticed something similar and posted about it on Google+: https://plus.google.com/u/0/103703080789076472131/posts/VhHE8TuJhcm.