Regents Recap — June 2012: Unscaled Graphs
Here is another installment from my review of the June 2012 New York State Math Regents exams.
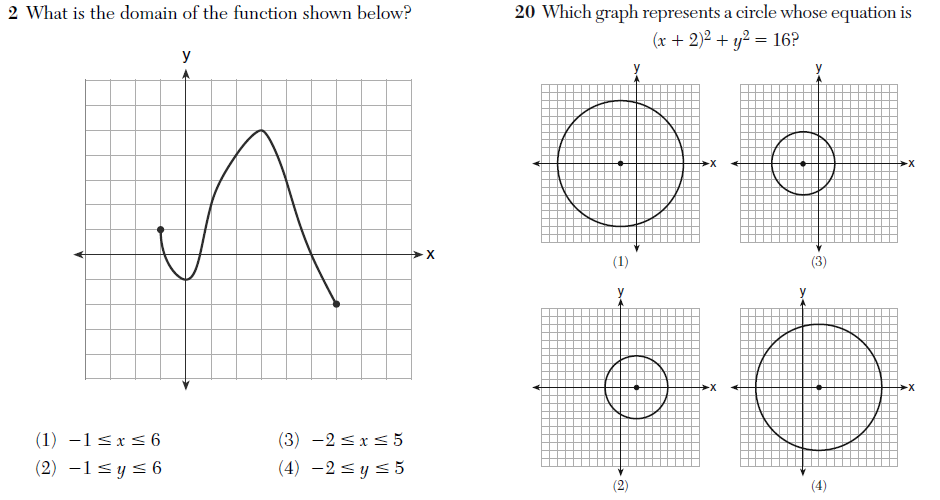
On the left is a problem from the Algebra 2 / Trigonometry exam; on the right, a problem from the Geometry exam.
Notice that no scale is indicated on any of the graphs here. That is, there is no indication of what “one unit” is equivalent to on any graph.
I admit that I’m pretty sloppy when it comes to labeling graphs, however I know some teachers make accurate labeling and scaling a point of emphasis when it comes to creating graphs. Properly understanding the scale of a graph can be of crucial importance, especially when trying to with questions pertaining to specific numeric values, as in these above.
Tests should stand as models of mathematical content and practice for students; they should not reinforce bad mathematical habits, like ignoring scale.
3 Comments
Ravi · August 24, 2012 at 2:14 pm
Just found your website. And I love it. I graduated as a engineer 20 years ago but stopped working as an engineer over 10 years ago and became a trade union official.
I still love maths but most of my maths is stuck at A level standard (calculus, basic stats, vectors etc). So the content of your blog is at the right level for me.
As for your comments you are dead right. Things that were drilled into me at secondary school (high school in US speak) were:
– label your graphs
– scale graphs properly
– always give units on the answer to any calculation
– always show your working
– if doing a calculation only quote the requisite number of significant figures (no spurious accuracy or necessary decimal places)
It was drilled into me and I am pleased it was. It lays the foundations of being able to do maths and provides a discipline and rigour that can be used in solving problems that are not mathematical.
If I had been given this question I would have made sure my answer said:
1. I think it is lazy and imprecise not to label the axes of the graph
2. To answer the question I will assume each square is one unit long and high.
But to be frank I cannot imagine any of my secondary school maths teachers ever setting a question with un-labled axes cos we were so well schooled in the basics, the whole class would have had a go at them for being so sloppy.
MrHonner · August 25, 2012 at 7:54 am
Thanks for sharing, Ravi, and for the kind words. Glad you like the site!
It’s definitely the sign of a good classroom when students hold the teacher accountable for their work. My students are quick to point out if I’ve made mistakes or been imprecise in how I’ve constructed or described a situation.
While mathematics is more than just the details, as you suggest, attending to the details helps create the right problem-solving environment.
Ravi · August 24, 2012 at 2:21 pm
By the way – I love the comment “human verification” test. Never seen one like that before