Replace Algebra with … Algebra?
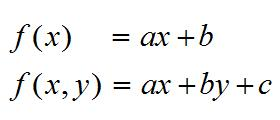Arguments that suggest we over-emphasize mathematics in education don’t bother me. I love math and see its utility in every aspect of my life, but I understand not everyone feels this way. Also, when someone says we shouldn’t teach math, or we should teach less, it encourages me to reflect on my own beliefs about math and teaching. This is usually a valuable experience.
So I read “Is Algebra Necessary?“, Andrew Hacker’s OpEd in the New York Times, knowing that I probably wouldn’t agree with much of it, but still prepared to examine my beliefs. Hacker offers up a few of the standard reasons why students shouldn’t be forced to take “Algebra” in high school (“it’s too hard”; “it turns kids off”; “not everyone’s going to be an engineer”), but he doesn’t really bring anything new or substantial to the discussion.
One thing I did find interesting, however, was Hacker’s suggested fix: instead of “Algebra”, we should be teaching courses like “Citizen Statistics”.
It could, for example, teach students how the Consumer Price Index is computed, what is included and how each item in the index is weighted — and include discussion about which items should be included and what weights they should be given.
This is indeed a good idea. Ironically, exploring the mathematics of the CPI is largely an algebraic activity.
Discussing which items should be included means creating a mathematical model and declaring variables for the unknown quantities we wish to investigate. These fundamental skills are taught and emphasized in high school algebra.
Determining the weights that these items should be given essentially amounts to finding the coefficients of some function of those variables and exploring the consequences of those choices. In their basic forms, these skills are also taught and developed in high school algebra.
Thus, it seems to me that Hacker is suggesting we replace Algebra, with, well, Algebra.
There are worthwhile discussions to be had about what we are teaching, why we are teaching, and how we are teaching. But those discussions should be led by people who really understand what’s going on. If Andrew Hacker thinks we should replace Algebra with Algebra, then someone else should be leading the discussion.
Related Posts
- Why Are We Listening to Andrew Hacker?
- Replace Algebra With … Algebra?
- N Ways to Apply Algebra With the New York Times
22 Comments
ihor (aka Climegy) · August 1, 2012 at 9:55 am
Replace Algebra with Algebra? Yes! But not by that title! Dont focus on Algebra in the traditional way which can be a very dull subject for most, but on something more intrinsically interesting like topics in statistics where you can discuss real world ideas and reveal to kids the power of algebra. Hacker does not mean throw out algebra with the bathwater he means teach it within a better context by using real world stuff that might interest kids more than just pure algebra which only a few of us really get. Then the algebra might actually become interesting to kids. In todays world there is room for more creative course offerings for kids that teach algebraic methods in lot more interesting ways than what all the publishers offer today under the title of Algebra.
MrHonner · August 1, 2012 at 10:05 am
Your claim that “Hacker does not mean throw out algebra with the bathwater” seems at odds with much of the sentiment of the essay. To me, Hacker’s answer to the question “Is Algebra Necessary?” is clearly “No”.
If, as you claim, all he’s really suggesting is that we need to show real-world applications of math to students, then he’s not really saying anything novel. And the point of my response is that it’s not clear he knows what he’s talking about when it comes to mathematics or teaching, so why should we listen to him?
ihor (aka Climegy) · August 1, 2012 at 10:24 am
I’m reading between the lines with Andrew Hacker. I’m sure he would agree with what I just wrote. We should listen to him because his question is legitimate and we as a math community need to seriously deal with it because we are losing too many students to the gatekeepers who push algebra as some kind of miracle drug for success in life. That is BS. In my 40 years as a math educator, I have seen too many perfectly capable people crippled by this algebra curse that it should be a gateway to future life. That’s what Im appalled about and that’s why Andrew Hacker and the many others who came before him with the same question should not be ignored.
MrHonner · August 1, 2012 at 10:47 am
As I see it, your point is that students should be exposed to mathematics in a engaging, compelling way, as this will motivate some of the challenging abstraction. Of course I agree with that.
To me, Hacker is making a very different point. As I read it, he is saying that understanding algebra isn’t necessary for most people, so it studying it shouldn’t be mandatory.
I agree with your points about mathematics instruction, but I do not agree that you are “reading between the lines” with Andrew Hacker. To me, you are ascribing to him an entirely different argument.
ihor (aka Climegy) · August 1, 2012 at 11:03 am
Interesting that you feel that way. I guess this will be a point of disagreement between you and me. I agree with hacker that algebra in its current form should not be mandatory. That does not mean that students should not do math! All im saying is that algebra that way it is packaged in 99% of the textbooks is anathema to me and should not be required of ALL college bound students. Science bound? yes of course.
Robert Berkman · August 1, 2012 at 11:13 am
I agree and disagree by distinguishing between algebra the noun and algebra the verb: one involves mastery of a set of rules using symbols; the second involves developing a certain style of thinking. Please check out my blog for more elaboration on this topic: http://bltm.com/blog/?p=139
Colin Beveridge (@icecolbeveridge) · August 1, 2012 at 1:17 pm
See, I look at something like this: http://www.cde.ca.gov/ta/tg/sr/documents/rtqalg1.pdf and say — in the nicest possible way — that you’re doing a bait-and-switch. Yes, CPI is an algebraic exercise. Yes, (a small) part of Algebra 1 is figuring out coefficients or modelling scenarios. But no, that’s clearly /not/ the focus of the algebra that’s taught in this module and I think it’s slightly disingenuous to point and laugh at someone for saying that it ought to be.
MrHonner · August 1, 2012 at 1:56 pm
Colin-
I appreciate your politely phrased criticisms. 🙂
First, I don’t agree that modeling with variables (aka “solving word problems”) and exploring functions (especially linear functions, like CPI) constitute only a small part of a HS Algebra course.
Second, as far as I’m concerned, the author’s answer to the question “Is Algebra Necessary?” is unambiguously “No.” Hence my confusion that the one example he conjures up as an alternative is, essentially, an algebra problem.
If Hacker’s argument is not “Algebra is unnecessary”, but instead “We should teach algebra in a way that is more applied and engaging”, then you are accusing the wrong person of the bait-and-switch.
William Hanisch · August 1, 2012 at 2:53 pm
In order for it to be a bait-and-switch there has to be bait. Where’s the bait? The percentage of kids, while in the 8th or 9th grade, who would BOTH not do well on the exam you posted AND be interested in how the CPI is calculated is so very minute–we’re taking some small fraction of one percent here–that it seems silly to call this a bait-and-switch. If basic algebra is too hard and too boring for a kid, what make’s you think this same kid would care about how certain economic indices are calculated? The real bait-and-switch here is the one by Hacker who as an adult seems to be interested in the CPI while forgetting what interested him as a freshman in high school.
The biggest part of Hacker’s opinion piece that bothers me is that underlying his words, he wants–as an adult–to be able to solve certain problems, and then blames the way algebra was taught for his (apparent) inability to do it. He seems to be thinking, “if only I learned how to solve *these* problems back in high school….” (Of course this is all disguised as algebra being too hard for other kids today.)
Algebra is an abstraction of basic arithmetic. With this abstraction comes the power to solve many, many problems. If we go back to treating every problem concretely, we lose the whole efficacy of the subject. Every new problem will seem just as hard as the last, with the underlying connections entirely lost.
I agree entirely that concrete problems should be presented and used to motivate the discussion. But once that’s done the subject should be treated abstractly (and have the kids practice so that they get comfortable with the abstraction). Additionally, every now and then a new concrete problem should be brought up to “drive the point home.” What Hacker is suggesting is 180 degrees different, that the actual algebra–the actual mathematics–should be relegated to the background and treated merely as a tool. This type of argument is exactly what got us here to begin with.
Kids now are discouraged to memorize the multiplication table, discouraged to become comfortable with fractions, discouraged to practice to get comfortable, and encouraged to use a calculator. After all, so the Hacker’s would say, arithmetic is just a tool to do the “real” problems. But if kids never become comfortable with arithmetic–including on fractions–how can they transition to the next level of abstraction which is algebra? They can’t, and this is a major reason why kids are doing so poorly.
Okay, I’ll stop my rant here. Sorry for such a verbose response. Perhaps I’ll write this up more completely into a proper essay.
MrHonner · August 1, 2012 at 8:35 pm
I’m glad to be part of sparking your outburst! Sounds like you’ve got your own response to write. Let me know when you post it. 🙂
slpinder · November 26, 2013 at 12:54 pm
As someone who spends every school day trying to convince high schoolers to care about algebra…and watching them struggle with the translation from words to math (always requiring help) and to watch them fly through the calculation once it is set up, I long for the days when students had a sense of satisfaction in solving “pure” math before tackling applied (word problem) math.
Colin Beveridge (@icecolbeveridge) · August 1, 2012 at 2:38 pm
And I appreciate your kind reply 🙂
Looking at the link I provided there, it’s question 10 before there’s any kind of real-life application, and 13 before anything that’s not pseudo-context. Eyeballing, that particular test (the first I found — it may not be typical) is about 10% reality-based, and very little of that 10% is any kind of question you’d ever want to work out in real life.
The vast bulk of that test is manipulation and vocabulary, when everyone would be better served if (as you suggest), students learn the power of math to solve problems they can relate to.
I still think it’s a bit strange to say you don’t see the difference between algebra as it’s seen by most non-mathematicians (that weird stuff with the xs that makes up 90% of that paper) and algebra that’s a useful tool to teenagers. Hacker’s possibly guilty of a minor vocabulary error, but I think mocking that looks like an attempt to distract from the issues.
MrHonner · August 1, 2012 at 4:45 pm
The author doesn’t understand what algebra is, or what’s taught in schools. This is not a minor vocabulary issue. This is a fundamental lack of understanding of the very topic he purports to be expert in.
He argues that algebra is unnecessary; then he proposes an “alternative” which he doesn’t recognize as an algebra problem. He refers to AP Statistics as a “backdoor” algebra class; it is not. He seems to believe that someone could really understand statistics or finance without understanding algebra; they could not.
Whatever the “issues” are, I don’t see why he should be speaking prominently about them.
mr bombastic · August 1, 2012 at 7:56 pm
Not quite sure what Hacker envisions for the CPI unit. I am guessing a spreadsheet with prices for different time periods and cells for weights that serve as variables. You could tinker around with the weights and see how the index is affected; do some research on why particular items are selected; select items and weights for a teenager CPI and see how well it compares to the actual CPI; etc. This may be a good use of time in a math class, but it could just as easily be done in a social studies class, and I don’t really think of this sort of thing as algebra. Seems more like computation to me, even though variables are involved.
Also, I am not at all opposed to integrating non-math topics into math class, but why is it such a one way street? Can’t Hacker just call for social studies teachers to do this sort of thing in their classes and make math optional?
MrHonner · August 1, 2012 at 8:44 pm
It doesn’t seem to me like he really put much thought into it; could be he felt obligated to offer up some “solution” in order to balance his opinion piece out. In the end, it’s just another recycled idea in a piece full of them.
Regardless of whether the ideas are any good, I don’t understand why he should be considered knowledgeable on the matter.
mr bombastic · August 1, 2012 at 9:32 pm
Agreed. I am not sure whether what currently passes for algebra should be required of all students, but Hacker did not come across as knowledgable of, well, anything in the article.
Ihor charischak · October 12, 2012 at 12:54 pm
Who cares whether Hacker is knowledgeable or not in all things algebra? He raises a legimitate question that I think that the more knowledgeable math community should not ignore that for most kids algebra is a waste of time. You are right what currently passes for algebra should be an optional course. The only subject that is important is the everyday math that Keith Devlin refers to. And if someone wants to take algebra at a future time more power to them. To me algebraic thinking is the kind of thinking you need to do to solve algebra problems. To learn how to do real world thinking you can do that through other subjects as you suggest.
MrHonner · October 12, 2012 at 2:25 pm
I care about Hacker’s qualifications. Public dialogue about teaching is largely dominated by people who have limited, or in some cases, no experience teaching.
Hacker’s editorial is yet another such example. Hacker does not know what algebra is. He is another non-expert framing and driving dialogue in education. This general trend is having a negative impact on schools, teachers, and ultimately students.
There are serious issues with math education, and important discussions to be had. Let’s strive for experts to lead these discussions.
Ihor charischak · October 12, 2012 at 9:29 pm
With all due respect my comment was intended for Mr. Bombastic. I think we have come to closure about this issue. My position is that I disagree with you on your assessment of the value of teaching traditional algebra to everyone and allowing only the experts to make that decision. Hacker is no dummy and his opinion should be respected. Again with all due respect if most teachers were as gifted as you are I wouldn’t even bring up the issue becuase then kids wouldn’t hate math as much as they do. Again, my only point is that algebra should not determine whether a student can proceed into higher education. There have to be other first class options for those students who view algebra only as impediment. Couldnt they get the kind of crticial thinking skills that supposedly algebra gives (and BTW there is no research that says definitely that it does) in ways that are more interesting to the student?
MrHonner · October 12, 2012 at 10:00 pm
Ihor-
I apologize if my remarks put you on the defensive. I tend to see the “Is Algebra Necessary?” episode in the context of the larger public smear campaign against teachers, schools, and public education in general. As such, thinking about it can fire me up a bit.
I understand the challenges facing math education. I’m not sure I would advocate that every student be required to take an “algebra” course, per se. But I do think every student should be consistently exploring ideas quantitatively as part of their education. That will necessarily entail learning, and doing, some algebra.
Ihor charischak · October 16, 2012 at 1:53 pm
Now we can agree to agree. 🙂 Thanks, for the response. You are definitely one of the “good guys.” I love your work.
2StepAlgebra · November 14, 2013 at 11:14 am
“The toll mathematics takes begins early. … one in four ninth graders fail to finish high school. … Most of the educators I’ve talked with cite algebra as the major academic reason.”
Indeed, the toll mathematics takes begins early… I teach at the high school level. It is amazing (frightening) how many children have not mastered arithmetic by middle/high school. Thus it is not surprising that they are stopped cold by algebra. The problem isn’t algebra, it is far earlier than that. Elementary arithmetic is not taught to mastery, is taught at a frighteningly slow pace, is not taught at the conceptual level, and is not taught by mathematicians. The consequence of entering middle/high school unprepared is very difficult to correct at the middle/high school level (remediation). I would suggest Elementary Mathematics Education is the actual major academic reason for failure, and that this is not uncovered until the graduation and college entrance exams reveal it – a decade later. The incorrect diagnosis, “I am bad at, and don’t like algebra” (actually a symptom)leads to the incorrect cure “remove algebra from the curriculum.”
The solution is teach kids to mastery at the early stages of the game. This builds the skills and confidence to continue and be successful. More and better math instruction, not less. But concentrate the effort at the early stages of the game, when it can be cured, and they have their whole academic lives ahead of them, not at the late high school end, when the children have lost interest and want to quit.