Are These Tests Any Good? Part 4
 This is the fourth entry in a series examining the 2011 NY State Math Regents exams. The basic premise of the series is this: If the tests that students take are ill-conceived, poorly constructed, and erroneous, how can they be used to evaluate teacher and student performance?
This is the fourth entry in a series examining the 2011 NY State Math Regents exams. The basic premise of the series is this: If the tests that students take are ill-conceived, poorly constructed, and erroneous, how can they be used to evaluate teacher and student performance?
In this series, I’ve looked at mathematically erroneous questions, ill-conceived questions, and under-represented topics. In this entry, I’ll look at a question that, when considered in its entirety, is the worst Regents question I have ever seen.
Meet number 32 from the 2011 Algebra II / Trigonmetry Regents exam:
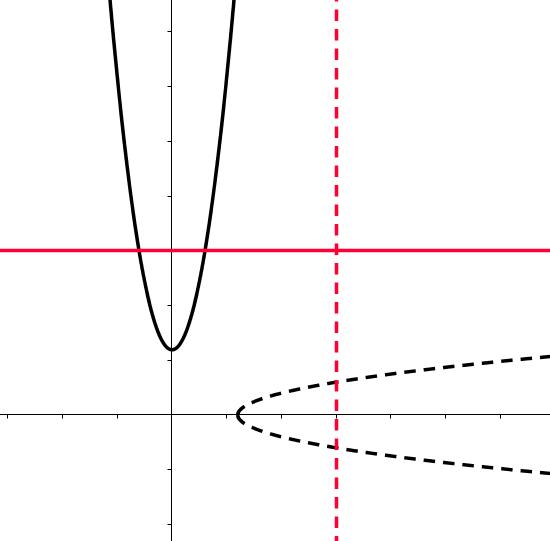
If , find
.
This is a fairly common kind of question in algebra: Given a function, find its inverse. The fact that this function doesn’t have an inverse is just the beginning of the story.
In order for a function to be invertible it must, by definition, be one-to-one. This means that each output must come from a single, unique input. The horizontal line test is a simple way to check if a function is one-to-one. In fact, this test exists primarily to determine if functions are invertible or not.
The above function fails the horizontal line test and thus is not invertible. Therefore, the correct answer to this question is “This function has no inverse”. And now the trouble begins.
Let’s take a look at the official scoring guide for this two-point question.
[2] , and appropriate work is shown.
This is a common wrong answer to this question. If a student mindlessly followed the algorithm for finding the inverse (swap x and y, solve for y) without thinking about what it means for a function to have an inverse, this is the answer they would get. According to the official scoring guide, this wrong answer is the only way to receive full credit.
It gets worse. Here’s another line from the scoring guide.
[1] Appropriate work is shown, but one conceptual error is made, such as not writing with the radical.
In summary, you get full credit for the wrong answer, but if you forget the worst part of that wrong answer (the sign), you only receive half credit! So someone actually scrutinized this problem and determined how this wrong answer could be less correct. The irony is that this conceptual error might actually produce a more sensible answer. The further we go, the less the authors seem to know about functions.
And it gets even worse. Naturally, teachers were immediately complaining about this question. A long thread emerged at JD2718’s blog. Math teachers from all over New York state called in to the Regents board, which initially refused to make any changes. A good narrative of the process can be found at JD2718’s blog, here.
The next day, the state gave in and issued a scoring correction: Full credit was to be awarded for the correct answer, the original incorrect answer, and two other incorrect answers. By accepting four different answers, including three that were incorrect, you might think the Regents board would have no choice but to own up to their mistake. Quite the opposite.
Here’s the opening text of the official Scoring Clarification from the Office of Assessment Policy:
Because of variations in the use of notation throughout New York State, a revised rubric for Question 32 has been provided.
There are no variations in the use of this notation, unless they wish to count incorrect usage as a variation. I understand that it would be embarrassing to admit the depth of this error, which speaks to a lack of oversight in this process, but this meaningless explanation looks even worse. This is a transparent attempt to sidestep responsibility, or, accountability, in this matter.
It’s not just that an erroneous question appeared on a state exam. First, someone wrote this question without understanding its mathematical consequences. Next, someone who didn’t know how to solve the problem created a scoring rubric for it, and in doing so demonstrated even further mathematical misunderstanding. Then, all of this material made it through quality-control and into the hands of tens of thousands of students in the form of a high-stakes exam. And in the end, facing a chorus of legitimate criticism and complaint, those in charge of the process offer up the lamest of excuses in an attempt to save face and eschew responsibility.
It might not seem like such a big deal. But what if your graduation depended on it? Or your job? Or your school’s very existence? Then it’s a big deal. At least, it should be.
Related Posts
8 Comments
jd2718 · August 30, 2011 at 11:41 am
And so just about every knowledgeable NY State teacher agrees, and yet….
I have three analysis books on my shelf, all allow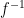 to be a preimage, and not a function. Marsden distinguishes between
to be a preimage, and not a function. Marsden distinguishes between 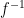 and the function
and the function 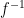 by writing “the function”:
by writing “the function”:
For and
and 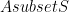 , we define
, we define 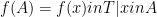 , and for
, and for  we define
we define  to be the set
to be the set 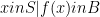 . We call f(A) the image of A under f and
. We call f(A) the image of A under f and  the inverse image, or preimage, of B under f.
the inverse image, or preimage, of B under f.
Note. We can form for a set
for a set 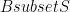 even though f might not be one-to-one or onto.
even though f might not be one-to-one or onto.
That is, of course, not what Albany meant, they were just wrong, but it makes the discussion more interesting.
MrHonner · August 30, 2011 at 12:32 pm
I guess the claim “there are no variations in the usage of this notation” is technically false, but how this notation is used in set theory isn’t any more relevant to this problem than the fact that raising something to the (-1) power often means “reciprocate”.
I see your point, but by my rubric their response still earns a 0 as “Completely incorrect, irrelevant, or incoherent”.
Dave Richeson · July 23, 2013 at 9:37 am
Of course, if you want to use the “inverse image” interpretation the domain and codomain of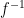 are no longer
are no longer 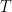 and
and  , but the power set of
, but the power set of 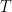 and the power set of
and the power set of  . So if that’s what they had in mind (which of course it isn’t) the question would have been to find
. So if that’s what they had in mind (which of course it isn’t) the question would have been to find 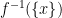 and the answer would be in set notation.
and the answer would be in set notation.
jd2718 · August 30, 2011 at 11:50 am
But the worst question? I’m going for Math B, June 2004, #33. (you have to scroll down to hit the right exam.
Inexcusably awful. Start with the arcs, get an answer. Or with the segments, get a different answer. Mix and match, get more answers.
(The problem can be solved with the measures given, only if you notice that they failed to to make the external segment tangent to the circle – in fact, that segment is nearly perpendicular to the tangent at that point…. Not their intent).
Jonathan
MrHonner · August 30, 2011 at 12:43 pm
I just noticed that you produced a similar series on terrible Regents questions from 2009.
http://jd2718.wordpress.com/2009/06/23/my-favorite-bad-exam-target-math-b-and-a-puzzle/
I guess things aren’t getting any better!
I’m not sure what the problem is with 2004 #33. I can’t the official test/rubric (your link doesn’t get me there). Is it the strong suggestion that PT is tangent to the circle, thereby encouraging students to use Power-of-a-Point? I don’t think anything in the given requires that PT be tangent.
jd2718 · August 30, 2011 at 1:45 pm
Here’s the naked link http://www.nysl.nysed.gov/regentsexams.htm Click Math B, then June 2004.
MrHonner · August 30, 2011 at 2:14 pm
Finally got through to take a look. So in the official answer key for the 2004 Math B, number 33, in order to find the length of PT they assume it is tangent to the circle. As you pointed out, the given information makes it impossible for PT to be tangent to the circle.
That is pretty bad. You’ve definitely got a case that this is the worst Math Regents question of all time.
In 2004, did the official correction begin with “Due to the variations in the ways segments intersect with circles across NY State…”?
jd2718 · September 5, 2011 at 9:35 am
They acknowledged that different approaches, assuming PT tangent, yielded different answers (in particular, beginning with the arcs vs beginning with the relationships between the lengths of the cords/secants/etc).
They never acknowledged that they had either 1) created a non-existent situation or 2) made a very very bad assumption about PT.