Are These Tests Any Good? Part 1
The test is a staple of modern education, and not just at the classroom level. Today, tests can determine which public schools a child can attend, whether or not a student graduates, which districts get state aid, and of course, which colleges might want you.
There is a movement afoot which seeks to legally tie teacher job performance to student test scores. There’s a simple argument at the core of this movement (“If students are doing poorly on tests, then the teacher must be doing a poor job”), and a simple counterargument (“There many factors beyond a teacher’s influence that affect student test performance”), but it’s a complex issue, and it has generated much controversy.
As the debate rages on in educational, political, and media circles, one particular aspect of this issue rarely gets discussed: test quality. If the tests being used to evaluate students, schools, and now teachers, are ill-conceived, sloppy, and erroneous, how legitimate a measure of teaching and learning could they possibly be?
In short, few people connected to this issue seem interested in the rather important question “Are these tests any good?”
I will address this question in a series of posts that examine the New York State Math Regents Exams. I’ll begin this series by looking at three questions from the multiple choice section of the 2011 Algebra II and Trigonometry exam. The official test and scoring guide can be found here.
First, an algebra question: which answer is equivalent to the given expression?
The “correct” answer, according to the scoring guide, is (1). However the real answer is that none of these are equivalent to the original expression. For two expressions to be equivalent, they must agree for every possible value of their variables. Let x = -1 and y = 1; the original expression evaluates to 2; the “correct” answer evaluates to undefined(or, if you prefer, to 2i). The two expressions, therefore, are not equivalent.
Now consider this question about graphs: which graph is not a function?
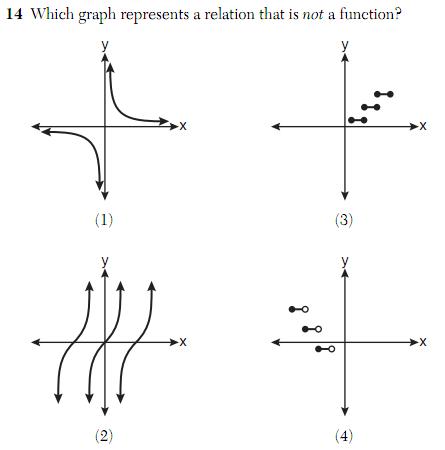A simple way to determine if a graph is the graph of a function is to use the vertical line test: if a vertical line can be drawn through the graph so that it intersects the graph more than once, then the graph is not the graph of a function. The “correct” answer according to the scoring guide, is (3), which is indeed not a function. But take a closer look at (2):
As the red vertical lines suggest, this graph also appears to fail the vertical line test. Therefore it is not a function. This question has two correct answers, only one of which was awarded credit.
Lastly, consider this question, again about graphs.
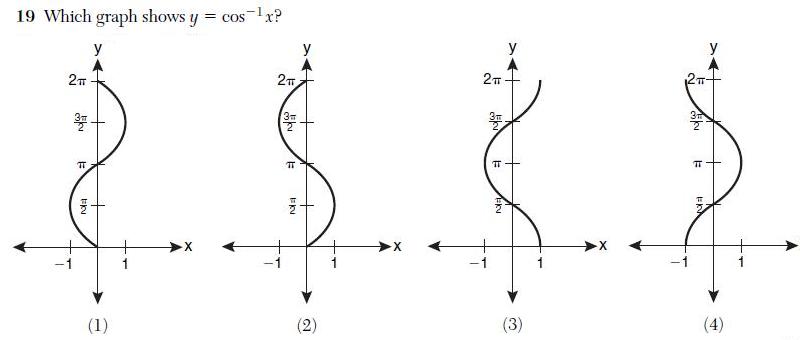As it turns out, none of these graphs is the graph of 
While it may seem that some of the issues raised here are merely technicalities, keep in mind that technicalities play an important role in mathematics. Furthermore, students who truly understand the relevant issues here might actually be at a disadvantage on these questions, wasting time sorting through these poorly-conceived problems and worrying about which answer to give.
A lot could be riding on this test: student graduations, teacher jobs, schools closings. With the stakes so high for so many, it seems like we should be paying closer attention to the question: Are these tests any good?
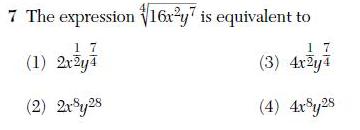
11 Comments
JBL · August 11, 2011 at 10:45 am
A small typo: I think you want a restricted range for
, not a restricted domain. (Or, rather, all the graphs in question have the appropriate domain.)
I thought Q 16 was the clearly most eggregious of the bunch (see http://jd2718.files.wordpress.com/2011/06/img_0353.jpg ); Q 20 has the same problem as 7, and the original answer key for Q 32 was terrible as well. Just absolutely embarrassing. (I read about this earlier at http://jd2718.wordpress.com another NYC math teacher blog.)
JBL · August 11, 2011 at 10:46 am
Gosh, I go to the trouble of using LaTeX and then I leave out the slash before “cos” — I hang my mathematician head in shame.
MrHonner · August 11, 2011 at 10:54 am
Thanks for the thoughtful remarks!
When I said “restricted domain,” I meant restricting the domain of the original function so that the inverse would be a function. I changed the wording to something more ambiguous so we can all be happy. 🙂
Question 16 was terrible, but at least the scoring guide gave credit for both correct answers.
The whole story around Question 32 is just awful. A true embarrassment. I’ll address the whole thing in a later post, but I made several comments on the blog you linked to when the discussion first started.
JBL · August 11, 2011 at 3:58 pm
I am fully satisfied with the resulting ambiguity :).
jd2718 · August 11, 2011 at 1:47 pm
The standards are lousy. The test design process is lousy (including no regularity to the distribution of question types). Important skills/topics are routinely omitted, and marginal or critical, every “PI” (performance indicator) has equal weight. We need, although I digress, to return to content-driven curricula in mathematics.
And finally the questions themselves are no better than a mixed bag. And the editing process is sloppy, and clearly involves far too few trained eyes. There may also be pressure to approve them quickly.
If this is the best New York State can do, than it should not be allowed to produce math tests. And I think this is the best New York State is capable of doing today.
Jonathan
MrHonner · August 11, 2011 at 2:31 pm
From a teacher perspective, I definitely see high-level problems in curriculum design for these courses, and the problems in the test-creation process you outline are evident to anyone closely connected to the issue. I guess these are the kinds of bureaucratic / institutional problems I come to expect operating in such a large system.
What really bothers me here is that these tests indicate a fundamental lack of mathematical understanding on the part of those who have created them. And it’s troubling to think that, ultimately, we as math teachers may be held accountable for it.
Alan · August 12, 2011 at 2:10 pm
These questions are regents-material worthy. I usually see such bewildering questions on practice regents exams with the correct answer not being as correct as you think. Seems that there’s more importance placed on AP exams and SATs that regents are just a joke. So why do we have them?
Anon · August 13, 2011 at 6:52 pm
Well, for question 14, your lines may make it look like there is more than one Y value for the same X value, but it seems obvious that the lines are merely supposed to be asymptotic.
MrHonner · August 13, 2011 at 7:22 pm
That those curves are supposed to have vertical asymptotes is likely “obvious” to a math teacher. And clever students will likely assume it as well, because they understand that when it comes to grades, figuring out what the teacher (or test) wants to hear is often as important as figuring out the correct answer.
That being said, the curves that are given are, in fact, not separated by vertical asymptotes, as demonstrated above. The question expects the students to apply the vertical line test, and a student doing so in earnest might get confused by the appearance of two correct answers.
You’re free to consider this nit-picking, but keep in mind that there is a conventional, unambiguous way to indicate vertical asymptotes on a graph: dashed lines. Their presence in this graph would remove the ambiguity; their absence is another indication of a genuine lack of mathematical understanding on the part of the exam creators.
Matthew · September 14, 2011 at 2:37 pm
Mr. Honnner,
I’ll see you and raise you one.
My daughter was given the Third Grade (2009) NY State math exam for practice last year. One of the questions asked her to use a ruler to measure an object that was 4 1/2 inches long.
Except the choices given were 4, 4 1/4 and a few extraneous ones.
I went through three different rulers in a failed effort, before determining that NYSED couldn’t even double check that they’d used a ruler properly.
And I thought, what of the poor third grader two years back, driving herself nuts to understand why the correct choice was not offered.
Keep up the good work.
MrHonner · September 14, 2011 at 10:32 pm
Thanks for adding your two cents, Matthew. By working my way through the many different issues with these exams. I really started to think about how these tests (and these significant problems) can have long-term negative effects on students.
Not only did your daughter suffer undue stress trying to find the right answer when it wasn’t there, but she was made to doubt herself for no reason. And she learned that sometimes the “right” answer is the one someone wants to hear, not necessarily the correct answer.
There are a lot of bad lessons being taught through these exams, and I don’t think it has to be that way.