Regents Recap, June 2017 — Assessing Irrationality
Despite its shortcomings, this kind of question keeps appearing on New York State math exams. This is number 27 from the June, 2017 Common Core Algebra exam.
Here’s an example of a full credit response according to the official model response set provided by the state.
There is no explanation here. The argument is simply It’s True Because It’s True: the difference between a rational number and an irrational number is irrational because the difference between a rational number and an irrational number is irrational. All the student has done is identified one number as rational and one number as irrational (without even identifying which is which) and recited the frequently-tested property.
As scored, this question is designed to test recall of a specific, incidental fact while intentionally avoiding the relevant mathematical content, namely, what it means for a number to be rational or irrational. A second model response that actually demonstrates some mathematical knowledge about irrational numbers earns only partial credit.
Unlike the student in the first response, or the test makers for that matter, the student here recognizes that the irrationality of the square root of 2 should be established. The explanation isn’t completely correct, but it demonstrates much more understanding than the first response. Unfortunately, as long as questions like this keep appearing on these exams, students and teachers will continue to be rewarded for mindlessly regurgitating what the test makers want to hear.
Related Posts
- Regents Recaps
- Regents Recap — January 2015: It’s True Because It’s True
- Regents Recap — June 2016: What Do They Want to Hear?
- Regents Recap — June 2014: Common Core Algebra, “Explain your answer”
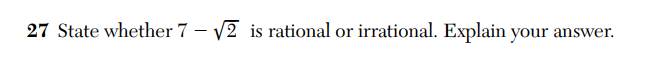
3 Comments
Anon · August 31, 2017 at 7:42 pm
I 100% agree.
If the point of the problem was simply “cite an appropriate theorem you learned”, as the first student did, then the second student did so as well, twice: She observed correctly that 2 is not a perfect square, cited the true theorem that square roots of non-perfect-squares are irrational, and then (like the first student) cited the theorem that the difference of a rational and irrational number is irrational.
I also agree that one would actually like to see a problem that asked students to grapple with the meanings of the words “rational” and “irrational”. But honestly, if the first student is correct I don’t see why the second one shouldn’t be.
Matthew Reardon · September 1, 2017 at 6:20 pm
Second answer is way better in my opinion.
Q A · September 11, 2017 at 9:25 pm
What’s infuriating to me here (as a college theoretical math major), is that it’s totally unclear what knowledge you’re allowed to assume in “explaining” your answer. Seems like clearly you were allowed to assume that the answer is true, meaning that the explanation is somewhat tautological.
But if you’re not allowed to assume that the answer is true, what are you? Can you assume that sqrt(2) is irrational, or do you have to prove that? I feel like that question (prove that 7-sqrt(2) is irrational) could be a reasonable homework question on a college intro to proofs sort of class! It’s definitely not trivial.