Regents Recap — June, 2017: When Side-Side-Angle is Enough

Published by MrHonner on July 24, 2017July 24, 2017

Here is yet another mathematically erroneous question from New York’s June 2017 Geometry Regents exam.

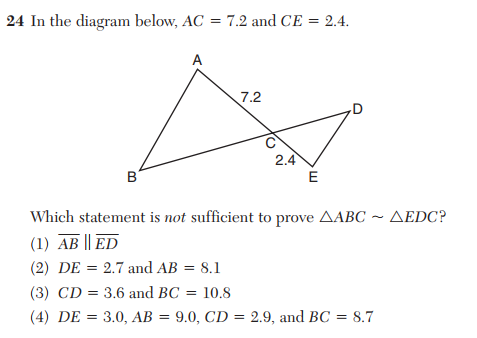
At first this question seems straightforward. There are several ways to determine if two triangles are similar, and the answer choices cover three of the basics: in (1) segment AB is parallel to segment ED, so congruent alternate interior angles can be used to show that the triangles are similar by Angle-Angle (AA); in (3) Side-Angle-Side (SAS) similarity can be used; and in (4), Side-Side-Side (SSS) similarity applies since all three pairs of sides are in proportion.

Presumably (2) is the answer choice that does not guarantee the triangles will be be similar, and according to the official scoring guide provided by the state (2) is the correct answer. But as it turns out, (2) is also sufficient to guarantee that the triangles are similar. This means that this question has no correct answer.

In (2), we have two pairs of sides in proportion and one pair of congruent angles (the vertical angles ECD and ACB). This is the Side-Side-Angle (SSA) scenario, and because this set of information does not determine a unique triangle, SSA alone is not sufficient to establish that a pair of triangles are similar (or congruent).

But there is additional information to work with in this question. The lengths of the sides of the triangles guarantee that angles B and D are both acute. This is because there can be at most one non-acute angle in any triangle, which is necessarily the triangle’s largest angle, and the largest angle in a triangle must be opposite the triangle’s longest side. Since angles B and D are not opposite their respective triangle’s longest side, they must be acute angles. And it turns out that this additional piece of information allows us to conclude that the triangles are similar.

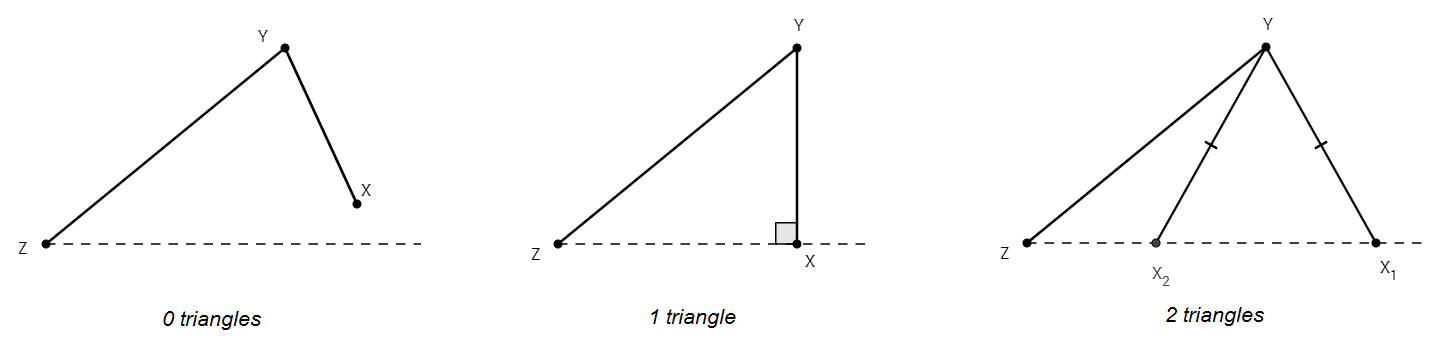
Here’s why. Suppose you know the lengths of segments XY and YZ and the measure of an acute angle Z. Depending on the length of XY, there are 0, 1, or 2 possible triangles XYZ. Here’s a geometric representation of all the possibilities:

This explains why SSA fails to uniquely determine a triangle: there may exist two different triangles consistent with the given information.

But if two triangles XYZ are possible, one of the triangles will have an obtuse angle at X and the other will have an acute angle at X. This means that if we happen to know that angle X is acute, then only one triangle XYZ is possible, and so this set of information (SSA and the nature of the angles opposite the given sides) uniquely identifies a triangle and can be used to establish similarity (or congruence) among a pair of triangles. Thus, the information in (2) is sufficient to conclude the triangles are similar, and so there is no correct answer to the above exam question.

Alternately, a more algebraic argument uses the Law of Sines. From triangle ABC we get

$\frac{sin B}{7.2} = \frac{sin ACB}{8.1}$

$sin B = \frac{8}{9} sin ACB$

and from triangle EDC we get

$\frac{sinD}{2.4} = \frac{sinECD}{2.7}$

$sinD = \frac{8}{9} sinECD$

And since

$\angle{ACB} \cong \angle{ECD}$

we can conclude that

$sinB = sinD$

Generally speaking we can’t conclude that the measure of angle B is equal to the measure of angle D: two angles with the same sine could be supplements or differ by a full revolution. But since we know both angles are acute, we can conclude that

$m\angle{B} = m\angle{D}$

Thus, the triangles are similar by AA. (This argument also shows that SSA together with knowledge of the nature of the angles is a congruence theorem.)

So, this high-stakes exam question has no correct answer. And despite the Change.org petition started by a 16-year old student that made national news, the New York State Education Department refuses to issue a correction. In fact, they refuse to acknowledge the indisputable fact that this question has no correct answer, perhaps because they don’t want to admit that a third question on this exam (see question 14 and question 22) has been determined to be mathematically erroneous.

UPDATE: All the media attention apparently convinced the NYSED to award full credit to all test takers for this erroneous question. Due to the discrepancy in wording, of course (link).

Related Posts

6 Comments

Ben · July 25, 2017 at 3:25 am

I think you mistyped in paragraph 2 and meant:
„ in (2) Side-Side-Angle (SSA) similarity can be used“

MrHonner · July 25, 2017 at 8:13 pm

No. SSA (by itself) is not a similarity (nor a congruence) theorem. But SAS (when the given angle is between the two given sides) is a similarity (and congruence) theorem.

MrHonner · July 25, 2017 at 9:22 pm

Ben-

I think I now understand. Someone pointed out that I had mistakenly referred to the non-erroneous answer choices as (1), (2), and (3) instead of (1), (3), and (4). I think that explains your legitimate criticism. Thanks for saying something.

Paul H · July 26, 2017 at 8:35 am

I believe this comes from insisting that SSA is some sort of renegade theorem that is best ignored entirely. I was taught this as well, way back in 1982 or so, and it was only when I looked at it recently that I realized that SSA is valid in some cases of A. (Then we teach HL, as if it’s some sort of strange random thing, when HL is SSA when A is right.)

If teachers are trained to think that SSA is always wrong, this sort of nonsense happens.

I wrote up the constraints on SSA with some visuals here: http://curiouscheetah.com/BlogMath/ssa-constraints/

William Hanisch · July 28, 2017 at 3:08 pm

Choices (1), (2), and (3) all depend on points A and E lying on the same line, and also points B and D lying on the same line. Is it de rigueur these days with the Regents Board to insist on assuming such things simply because the look that way in a diagram? Or dismiss complaints to the contrary as being unnecessarily pedantic? If I recall correctly, when I took the Regents back in the 1980s the wording of such a problem would include something like: “Line segments AE and BD intersect at point C.”

MrHonner · July 28, 2017 at 7:22 pm

William-

What you are suggesting–making diagrams unambiguous through precise mathematical statements–is dramatically beyond the level of rigor of current Regents exams. You can see my most recent post (here) and the associated links for some examples of the lack of precision routinely found in these exams.