Regents Recap — June 2016: Algebra is Hard

Published by MrHonner on August 1, 2016August 1, 2016

In my ongoing analysis of New York State’s math Regents exams, the most discouraging issues I encounter are the mathematical errors. Consider this two-point problem from the June 2016 Common Core Algebra 2 exam.

There are no issues with this simple algebraic identity, but there is a serious issue with how this problem was graded.

With each exam a set of model responses are published by the state. These serve as exemplar student work and inform graders of what correct and incorrect responses look like. Here is a model response for this problem.

Sadly, according to the official scoring guidelines, this perfectly valid and 100% correct response earns only one point out of two.

The purported reason for the penalty is that “The student made an error by not manipulating expressions independently in an algebraic proof”. It’s unclear what, if anything, this means, but there is no requirement that expressions be manipulated independently in an algebraic proof. This is an artificial criticism.

I suspect the complaint has to do with multiplying both sides of the equation by some quantity. I have occasionally heard teachers argue that, when proving an identity, you can’t multiply both sides of an equation by the same thing. Their reasons vary, but the most common explanation is that in doing so you are assuming the sides are equal, which is what you are trying to prove.

This is faulty mathematics. For the most part, there is no issue with multiplying both sides of a purported identity by the same quantity: if the original equation is true, the new equation will be true, and if the original equation is false, the new equation will be false. In general, the equations are logically equivalent, that is, true and false under exactly the same circumstances.

For example, consider the true equation 4 = 4 and the false equation 4 = 5. Notice that

4 = 4 and 3*4 = 3*4

are both true, and

4 = 5 and 3*4 = 3*5

are both false. Multiplying both sides by 3 does not change the truth value of either equation.

Now, I said for the most part because there is one particular situation in which multiplying both sides of an equation by the the same quantity can be problematic. Multiplying both sides of an equation by zero can turn a false equation into a true equation. For example

3 = 2

is clearly false, but

0*3 = 0*2

is true.

So, the full mathematical story is that the statements a = b and ka = kb are logically equivalent if $k \neq 0$ . That is to say, multiplying both sides of an equation by the same quantity will preserve its truth value if you aren’t multiplying by zero.

Let’s return to the model response in question. We have

$\frac{x^3 + 9}{x^3 + 8 } = 1 + \frac{1}{x^3+8}$

$(x^3 + 8)(\frac{x^3 + 9}{x^3 + 8 }) = (x^3 + 8)(1 + \frac{1}{x^3+8})$

Here, both sides of the original equation have been multiplied by $(x^3 + 8)$ . As long as $x^3 + 8 \neq 0$ , these two equations are logically equivalent, and so proving that the latter equation is an identity is equivalent to proving that the original equation is an identity.

Could $x^3 + 8$ equal 0? Generally speaking, yes. But conveniently, the exam authors went to the trouble to tell us that $x \neq -2$ , which means $x^3 + 8 \neq 0$ . Therefore, the mathematics of the model response is perfectly valid. It should earn full credit.

The error in these official grading instructions demonstrates a serious lack of mathematical understanding on the part of those who produce these exams. Errors like this, and this, and this, should give pause to those who automatically assume that exams like these are valid measurements of mathematical knowledge and ability.

And there are serious and real consequences here. Not only are student losing points for perfectly valid mathematical work, official state documents are demonstrating incorrect mathematics to classroom teachers. Without correction, this erroneous mathematics will likely be passed along to students.

While there can be legitimate disagreement and debate about the extent and use of testing in education, I think we can all agree that the tests themselves should not undermine the teaching and learning of content. And that’s exactly what errors like this do.

Related Posts

Categories: TeachingTesting

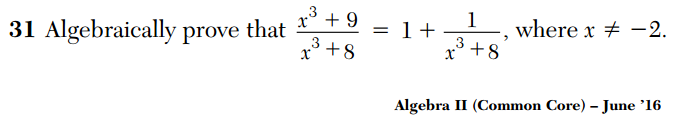
41 Comments

Amy Hogan · August 1, 2016 at 10:04 am

I’ve been waiting for you to write about this one. It’s wrong, just wrong. Crossing fingers that graders missed this one-point deduction at quick inspection?

MrHonner · August 1, 2016 at 12:44 pm

It’s sad that we have to hope for incompetence on the part of the graders. As we’ve discussed before, inconsistent grading across the centralized scoring centers in NYC (and across the state, for that matter) is its own serious problem.

DAVID MARAIN · August 1, 2016 at 11:10 am

Life was so much easier for testing companies when assessments/scoring were hidden! ETS had to acknowledge their errors too! But I have a different question. Where exactly in the Standards is the topic of Proving Algebraic (non-trig) Identities? Exact wording? Requirement of “manipulating one side at a time”? This was traditional with trig identities but, as you accurately pointed out, multiplication of both sides by a nonzero quantity is mathematically valid.

MrHonner · August 1, 2016 at 12:54 pm

As I’ve said many times, despite my criticisms of the NY Regents exams, I am thankful they are made public. The situation is undoubtedly worse with private, for-profit interests in charge, which is where we’re headed I’m sure.

HSA.APR.C.4 is the most relevant standard, I think: “Prove polynomial identities and use them to describe numerical relationships. (Link: http://www.corestandards.org/Math/Content/HSA/APR/C/4/)

This artificial restriction is only traditional with trig identities because most quantities involving trig functions can be zero, and so disposing of those cases can be tedious. Still no excuse for introducing an artificial rule.

DAVID MARAIN · August 1, 2016 at 11:40 am

Follow-up to previous comment…
What would scoring have been in the unlikely event that a student added,”Since x³+8≠0″??

John Chase · August 1, 2016 at 8:59 pm

My comment didn’t render correctly… the iff symbols are missing between the letters in a lot of places. Here it is better:
——-

I don’t want to start a fight, but I’m going to step out and say that I actually *agree* that this student’s work is incorrect. It’s not a damning error, but I do believe it represents a logical mistake on the part of a student.

When we “do algebra” by performing algebraic manipulations to both sides of an equation to transform it from equation A into equation B, we always mean A => B, we don’t mean A⇔B. Take, for example, the following algebra which results in an extraneous solution:

sqrt(x)=-5
(sqrt(x))^2)=(-5)^2
x=25

In this example, each line follows from the previous, but reversing the logic doesn’t work. But we accept that this is the usual way we do algebra (A => B => C). Here C doesn’t hold, however, because A is false.

So if this is the universal way we interpret algebraic work, which is what I argue, then I think it’s wrong to construct an argument of the form A => B => C in order to prove statement A is true from premise C. The argument begs the question.

It’s just bad style, I say, to start a proof by saying “I’m about to prove statement A. Let’s first start by assuming that statement A is true…”

I encourage my students to work with only ONE side of the expression and manipulate it independently, in its own little dark box, and when it comes out into the light, if it looks the same as the other side, you’ve proved the equivalence of the expressions.

For example, to show that log(1/(t-2)) – log(10/t) = -1+log(t/(t-2)) for t>2, I would expect this kind of work for “full credit”:

LHS = log(1/(t-2)) – log(10/t)
= -log(t-2) – log(10) + log(t)
= -log(10) + log(t) – log(t-2)
= -1 + log(t/(t-2)
=RHS

Interestingly, I WOULD also accept an argument of the form A⇔B⇔C as justification for conclusion A from premise C, but I would want a student to say “A is true if and only if B is true, which is true if and only if C is true.” Of course, I do not encourage this somewhat cumbersome construction.

I would also accept the argument if it started with the line x^3-8=x^3-8 and the other lines followed, in reverse order (C=>B=>A).

The way we normally read algebra is with “implies” not “if and only if,” which is why I say the student work is wrong. (Again, not super-duper wrong, but wrong enough that I would correct it.)

My apologies for the long comment!

Andrew Knauft · August 1, 2016 at 10:41 pm

I echo this position. In fact, I go so far with my students as to insist on logical connectives (words or symbols) whenever they craft proofs in this manner. (Grading the inevitable “mistakes” is a different issue…) However, I don’t believe this is the conceptual error referenced by the scoring guidelines.

Reading the test commentary, this question was placed in order to assess A-ASSE.A.2: “Use the structure of an expression to identify ways to rewrite it.” This response, rather than manipulating the forms of the expressions on the left and/or right until they were identical, treated the whole equation as the expression to be manipulated. The steps show that this student is aware the truth-value *of an equation* does not change when multiplying by (non-zero) expressions; the steps do not show that this student is aware that *expressions* remain the same when multiplied by (clever forms of) 1. A fine point, to be sure, and absence of evidence is not evidence of absence. Knocking this answer down to half-credit because of such a restrictive interpretation of the standard seems extreme too me.

MrHonner · August 2, 2016 at 9:59 am

Andrew-

The directive of the problem is clear: prove that the equation is true. Nowhere does it state that the student must use the structure of an expression to identify ways to rewrite it. [Moreover, it’s not clear to me that this work isn’t an example of that standard.]

If scoring guides are going to prioritize particular methods, then that must be made clear in the statement of the problem. Otherwise, it’s a terribly unfair game of “guess what the test-writers want to hear”.

RR · August 6, 2016 at 2:20 pm

It is a subtle but important point that equations *are* statements with a truth value. For example, 1 = 1 is true and 1 = 2 is false. Equations with variables also follow this logic once we specify the domain from which the variables are chosen. For example, x = x+1 is false for all real numbers x.

Thus, starting with the equation is *absolutely* the same as “starting with what you want to prove”. Experienced mathematicians sometimes do this with both equalities and inequalities so that we can get an idea of how a rigorous proof will go, but it certainly does not qualify as a rigorous proof.

So, I agree with the test, both with the way it’s phrased and with the assessment of the incomplete answer. But I despair that this basic idea is not being taught in US algebra courses.

Nick · August 6, 2016 at 6:51 pm

The example wasn’t a proof though.

MrHonner · August 2, 2016 at 9:46 am

I appreciate this different perspective, John, and that you have provided such a thorough response.

First, I think it’s false that “we always mean A => B” when we “do algebra”. Much of what we do when we transform equations produces logically equivalent statements, which take the logical form A <=> B. So I definitely reject your claim that this is the “universal way we interpret algebraic work” (which is very strong claim indeed!).

The example you provide (squaring both sides of an equation) is a classic example of a situation in which the two equations are not equivalent. But to my point, this would certainly not be valid in proving an algebraic identity.

Second, I think there are two important distinctions to make. And I think they are somewhat related.

The first distinction is between “what is meant” and “what is valid”. I think it’s hard to dispute the mathematical validity of the sample response: correct algebra has produced a sequence of equivalent equations that link the initial equation to an obvious identity.

Now, you are free to argue that the student has failed to demonstrate what exactly this work means. But if you look at the full-credit model responses, you’ll find that none provide any explanation of what the algebra means. Why is this particular work held to a higher standard? I think the response is convention, and I don’t think that’s a valid reason.

The second distinction is between what we expect students to do in our classes and what we expect students to do on standardized exams. How you and I teach students to approach such problems, and what we expect of them, is necessarily different than what should constitute valid and correct work on a standardized exam.

I’m definitely not arguing that this is exemplary work. I expect more from my students than this, and I’m sure you do, too. But I am arguing that this is as valid as any of the other full-credit model responses provided by the state.

Thanks again for your thought-provoking, civil, and well-presented response!

John Chase · August 2, 2016 at 11:13 am

I guess I’d make an even broader claim: ANY time we see a sequence of statements (not just equations) A, B, C that is being put forward as a proof, if logical connectives are missing, the mathematical community agrees that “=>” is the missing logical connection.

That is, if we see the proof A,B,C as a proof of statement C from premise A, we assume that the argument really means A=>B=>C.

This is usually the interpretation in the typical two-column proof, too. We just provide the next step with a supporting theorem/definition/axiom, but we don’t also go out of our way to say “oh, and line #7 follows from the previous lines.”

Example: Given a non-empty set E with lower bound a and upper bound b, show that a<=b.

1. E is non-empty and a and b are lower and upper bounds for E. (given)
2. Set E contains at least one element x. (definition of non-empty)
3. a <= x and x <= b. (definitions of lower and upper bound)
4. a <= b. (transitive property of inequality)

Notice I never say that one line follows from the next. And also notice that it would be a mistake to interpret the logical connectives as biconditional.

…

And yes, thanks for the civil conversation. Reflecting on our practice, and on mathematics itself, is what teachers do!

David Richeson · August 15, 2016 at 11:25 pm

Hi Patrick,

Thanks for the interesting post and for sharing your thoughts. I’ve read some of the comments here and I find them very interesting and thought provoking. However, I have to admit that I disagree with you, and I agree with John Chase quite strongly. In fact, I work very hard to break students of writing exactly this type of argument. If they had put “if and only if” between each line I’d feel better, but even still it isn’t great. The x≠2 bit makes it messy. The first two expressions are equal for all x≠2, but the last two are equal for all x. I’d much rather see a string of equalities that starts with the LHS and ends with the RHS.

I wrote a (now that I reread it seven years later, somewhat obnoxious) blog post about this in 2009 https://divisbyzero.com/2009/12/27/showing-two-expressions-are-equal-stop-the-madness/. (Interestingly, John Chase’s father Gene Chase commented on the post!!) In fact, your example is a better example of what I don’t like than the example that I gave in my blog post.

As a final comment, I also don’t like the question. I don’t like the “where” construction. It isn’t terrible, but I try to discourage students from using it. It is too easy for them too confuse themselves with how it fits in with the quantifiers. I’d much rather see “if x≠2, then…” or “for all x≠2…”

Dave

MrHonner · August 16, 2016 at 8:00 am

Thanks for chiming in, Dave.

I feel like most of the apparent disagreement about this post comes from people talking about different things.

You, John, and many others have offered thoughtful criticisms about this work as a *proof*. In particular, your post about this kind of problem is spot on.

I, on the other hand, am evaluating this work as a response to an exam item. My point is not that this is a good proof (it isn’t), but that it is not invalid for the reason officially cited, and thus, it is as valid as the other responses that were awarded full credit (none of which would meet any commenter’s criteria of a good proof).

Jerome Dancis · August 1, 2016 at 9:30 pm

I’m curious to see what a full credit correct solution looks like. Does it include mentioning the Distributive Rule.
I told my students that after doing that calculation, they should number the steps 1 to 4 starting from the bottom! Of course, crucial to mention that x is not -2 when going from Step 3 to Step 4.

MrHonner · August 1, 2016 at 9:36 pm

You can find several examples of full credit solutions in the Model Response Set, found here: http://www.nysedregents.org/algebratwo/

DAVID MARAIN · August 1, 2016 at 11:13 pm

After reading Mr. Chase’s comment I’m rethinking this. Consider proving the identity: 1/(x²+1)+1/(x²+1)=2/(x²+1)
Multiplying through by (x²+1) produces a DIFFERENT identity 1+1=2, even though the steps are reversible. Stating the 2nd equation is an identity is not a “proof” of the original. Subtle point here but worth discussing further…

MrHonner · August 2, 2016 at 7:01 am

All true identities are equivalent to, say, the equation 1 = 1, but knowing 1 = 1 doesn’t prove all true identities. However, if through algebra you establish that two equations are equivalent, then showing one is an identity is sufficient to showing the other is an identity.

Mistercorzi · August 2, 2016 at 3:48 am

Following on from John’s comment above. The proof as written has no logic connectors => or and therefore “common usage” comes into play i.e. the assumed connector is => unless otherwise stated. Hence the student has implied a true statement from a statement whose truth is not known. Logic dictates that from a false statement anything can be implied (truth or falsity). So with the normal reading of this “proof” i.e. implication ( => ) where each line is implied from the previous line, it is clear the identity has not been proved especially since there is no indication that the reverse implications have been considered by the student. Since there are only 2 points allocated for the proof a score of 1 seems reasonable and fair.
Suppose for a moment that the order of the four written lines were reversed with the first line (now the last line) reading “divide both sides by x^3+8”. This proof would be applauded as mathematically correct and awarded 2 points. Again the assumption on the part of the reader is that each line is implied by the previous line.
I think the justification in the exemplar material for only gaining 1 mark is lacking clarity and the logic issue as explained above needs to be central if the student is to learn from the material.
The process of proof is beautiful but difficult – we should celebrate these difficulties as that is where true learning lies!

MrHonner · August 2, 2016 at 10:06 am

I think I’ve responded to most of this in my response to John, but I don’t accept these notions of “common usage” and “normal reading”.

You are free to argue that there are no indications that the [completely true] “reverse implications” have been considered, but there is no indication in any of the model responses that any consideration has been given to the logical connections between the statements.

anon · August 2, 2016 at 7:08 pm

I agree with Mr. Honner that the grading guideline “The student made an error by not manipulating expressions independently in an algebraic proof” is meaningless nonsense.

But I think I also agree with Mr. Chase that the natural way to read a proof like this is that each statement follows from the previous ones. (For what it’s worth, I’m a professional mathematician, although that certainly gives me no special insight into pedagogy or testing.)

There’s no objective definition of what constitutes a proof; it’s a convincing explanation for humans, hence a human construct. But for me one reasonable standard is that a proof shouldn’t make me say “so what?” at the end, which this one does. That could’ve been avoided with a few words at the end.

To put it another way, this proof gives me no information either way as to whether or not the student wrongly believes that “P implies Q and Q is true means that P is true”. And isn’t this exactly the type of thing we are trying to test when we ask students to prove things? (I am perfectly willing to believe that the “correct” answer doesn’t indicate this either, which is may be a different fault of the grading guidelines.)

On the other hand, maybe this is unfair to ask in a timed standardized test.

MrHonner · August 2, 2016 at 8:58 pm

I appreciate your perspective as a mathematician (and appreciate, even more, your acknowledgment that being a mathematician doesn’t guarantee expertise in teaching math!).

I’ve found myself defending this response more than I intended. My primary point is not that it is an exemplary proof, but that (1) it is as mathematically valid as the other responses that were awarded full credit, and (2) a bogus criticism is cited as reason for the penalty.

No, the work does not indicate whether the student wrongly believe that P => Q and Q entails P. But as I’ve argued elsewhere, I don’t think any of the full-credit exemplar work would pass such a standard. And I’m sure reasonable people could be left wondering “So what?” after reading them, as well.

anon · August 2, 2016 at 11:16 pm

Fair enough. It’s a bad pairing of test question and official answer key.

I guess my point is this: If you ask students to prove things, then you should have some kind of standards for the quality of their explanation (and make that part of the curriculum), which clearly even the “correct” answers don’t do.

On the other hand, maybe you think this is unreasonable, especially for a single minor question on a timed standardized test. Fine! Then if all you’re expecting them to do on this question is correctly manipulate algebraic symbols (perfectly fine), then just ask them to do that.

E.g. If x is not -2 and (x^2+9)/(x^2+8) = 1/y, find y as a function of x.

anon · August 2, 2016 at 11:17 pm

Sorry, my original answer was eaten by the capcha and I mistyped my example the second time:

If x is not -2 and (x^3+9)/(x^3+8) – 1 = 1/y, find y as a function of x.

DAVID MARAIN · August 3, 2016 at 11:56 am

The diversity of opinion among professionals here reinforces Anon’s comment re clarifying the standard for proving identities. Each standard to be assessed needs these guidelines for all stakeholders including the test makers and scorers. I contacted a Boston College Math Prof and he allowed me to share this Ishared a similar problem with him and I still have a logic point to make beyond his response but I found it fascinating:

Anyway, dividing both sides of a known identity by the same expression is certainly valid! To be really pedantically precise, it is saying that for any functions f, g, h, if f(x) = g(x) for all x, then it follows that for all x with h(x) non-zero, f(x)/h(x) = g(x)/h(x). This in turn is straightforward to prove by applying the corresponding number fact ”if a = b and c non-zero, then a/c = b/c” to any arbitrary value of x.

But all that isn’t the point, I imagine. I don’t really know what the grader had in mind, but maybe they were looking for a sequence of expressions

f(x)/h(x) = … = … = … = … …=. .. = g(x)/h(x)

where each new expression is a valid manipulation of the one before it. Why they would insist on that form is totally beyond me— I completely agree that “doing the same thing to both sides” is as valid as stringing together expressions. It IS true that if you do the same thing to both sides of a known identity, then you can NOT express the proof by putting equal signs between every expression written in the proof, and since that form of algebraic derivation [i.e. …=…=…=…=…=] is popular with students and teachers, perhaps they were aiming for methods that “transform one side into the other” rather than the slightly more abstract approach of deriving the identity from another known identity by doing the same thing to both sides. Or maybe some teachers don’t want to fuss about “not writing equal signs between everything, always” and therefore insist on derivations that permit it, which in effect means you never “do the same thing to both sides” (definitely the wrong way to teach, in my mind, but I could imagine it)

At any rate, my view is that there is nothing better mathematically, pedagogically, logically, or any other way, about stringing together equal expressions vs. deriving new equations from old ones by doing the same thing to both sides. In fact, I think it’s important to do both, rather than try to force every algebraic derivation into one format. There’s always more than one correct derivation and understanding why various methods are correct is way more important than being able to solve a particular problem by a predetermined method or format.

I think the student should have gotten full credit (assuming that the distributive laws used in both steps are “obvious” enough not to require citing).

Best to you, Dave…..Ned

John Chase · August 3, 2016 at 1:43 pm

David, I think everyone would agree that we may “do algebra” to both sides of a *known* identity.

But if the task is to prove a purported identity, then one may not *start* a proof with the assumption that it is already true. Agree?

DAVID MARAIN · August 3, 2016 at 2:21 pm

Of course John and that’s why I stated I had an additional point to make! The student needs to state that the reasoning proceeds from the “bottom up”, something like this: P(x)=Q(x) for all x≠-2 because, for k≠0, k•P(x)=k•Q(x), for all x≠-2. The issue for me is that this depth of logic was assigned only 2 points. If this were a 3-pt question I’d have been comfortable awarding 2 pts because the logical connection wasn’t stated. Further what exemplars for this type of proof were provided to educators and the public beforehand? Have verification of non-trig identities been a mainstay of the curriculum and assessment for some time?

John Chase · August 3, 2016 at 2:33 pm

Okay, I’m with you then. I agree that the original work written in reverse would be acceptable, OR, as you say, a written note from the student saying that the argument is to be “read in reverse.”

I also agree that the fact that this is a 2-point question makes things tricky, and taking off 1 out of 2 points might be a bit harsh!

As far as exemplars go, I feel like this discussion *should* be present in all math classrooms. Verification of this kind of “algebraic” identity has long been a part of AP and IB curricula (and our own district’s curriculum), and I don’t think it’s too high of an expectation for all students.

And for what it’s worth, I think AP/IB wouldn’t accept this student’s work either. The AP/IB graders would want to see something that constitutes a proof–something of the kind we’ve been suggesting in our comments.

DAVID MARAIN · August 3, 2016 at 4:34 pm

I never thought we were really at odds! I was just curious about how Common Core has affected this in the last 3-4 years. These types of exchanges on Patrick’s excellent blog should definitely be played out in *every* district. Based on my experiences there needs to be much more of this! I’m all for setting the bar high provided we move toward a more level playing field. We’re not quite there yet… And, Patrick, thank you for enabling this. Your insights and astute comments are provocative and refreshing!

John Chase · August 3, 2016 at 8:28 pm

Amen, amen, amen, to all of that.

Next goal is for all of us o bring this discussion into our departments a d districts, as you say…or get them all out here to the MTBoS!

Dylan Kane · August 4, 2016 at 12:46 am

I’m really enjoying learning from the thoughtful people commenting above. I had never thought in this much depth about what it means to prove an identity; thanks to all of you for pushing my thinking forward.

I teach this in the context of trig identities, and my experience is that the idea that we can’t work on both sides of the equation is one of the hardest for students to understand. I can provide counterexamples for students where things go wrong and that may be helpful, but doesn’t solve the problem.

But let me put forward an example of student work I see quite often in this context (which is a only a bit contrived to make my point):

Prove:
cosx * sin^2x + cos^3x = 1/secx

Solution:
cosx(sin^2x + cos^2x)=cosx

cosx = cosx

It drives students nuts that this might me mathematically incorrect, yet clearly logical. It’s challenging to provide enough examples of places where logic that students see as similar to this go wrong. I don’t think that, at the high school level, holding resolutely to this standard of mathematical rigor is actually promoting sense-making or reasoning from students. I see its value from a mathematical perspective, but not from a pedagogical one.

Just my two cents.

MrHonner · August 4, 2016 at 8:31 am

Dylan-

The notion that “we can’t work on both sides of an equation” in proving an identity, like the notion that we can’t multiply both sides of an identity by the same non-zero quantity, is a convention, not a mathematical rule.

The only thing mathematically incorrect in your example is that you have replaced an expression with something that it is not identical to: namely, you have replaced 1/sec(x) with cos(x). These two expressions are not identical, because cos(x) is defined for all real x, whereas 1/sec(x) is undefined for many values of x.

Your example is, in fact, not an identity, for the same reason. The equation is not true for all values of x, for example, x = pi/2.

DAVID MARAIN · August 4, 2016 at 9:06 am

Just when I thought we’d moved on!
I needed to go back to my basic understanding of an algebraic identity, its meaning and its purpose for the curriculum. Let’s consider 2 functions P(x) and Q(x). We want students to know that if we can verify they have the same numerical value for all x in their common domain then P(x) can be replaced by Q(x) using substitution. Rewriting algebraic expressions in equivalent forms is a central part of math & a critical skill. Once we make “simplifying”/”rewriting”/”substituting” the focus the perspective changes. The formal and traditional mechanisms of transforming P(x) to be identical in form to Q(x) is because of this perspective in my opinion. Further this is why mathematicians often use 3 bars instead of “=” to denote an identity to distinguish it from an ordinary “conditional” eqn like 3x-6=0. I would then argue that we can express the problem as “Transform P(x) into Q(x) using algebraic rules and known identities” and drop the “=” entirely! This would remove the issue of what you can do to “both sides of the equation”. Yes, I’m suggesting a change in the curriculum. Oh my!!

Jonathan Halabi · August 4, 2016 at 9:01 am

Patrick,

this is a NY State conceit. It predates the standards-based exams.

When I became a math teacher in 1997, I was shocked by “mathematical rules” that seem to have arisen among NY State’s Education Department and the mathematics teachers of NY State, but nowhere else.

This (identities are proven by manipulating each side of the equation independently, and do not allow the “addititive property of equality” or the “multiplicative property of equality) is one of them.

MrHonner · August 4, 2016 at 1:44 pm

Several interesting conversations have emerged from this thread, however they’ve strayed from evaluating this work in the context of this particular standardized exam.

Allow me to return to that context. I’ve heard two primary criticisms of this work (each coming from multiple sources):

(1) By writing the equation at the beginning, the student assumes the equation is true.
(2) The “proof” is actually written backward. In order for the logic of this work to be valid, you would have to read it in reverse order.

I don’t find these criticisms compelling, and here’s why: consider the work below (or at this link.)

The above criticisms both apply to this response. Yet I suspect that most math teachers would award full-credit for this work.

John Chase · August 4, 2016 at 1:56 pm

I would discourage a student from doing this, too. It’s problematic because the first thing the student writes down is the very thing they’re trying to prove, as you’ve already pointed out. I’m curious how many math teachers actually see this student work as a valid, well-formed proof.

I’m not sure how I would score it, however. I might let it slide and just add a written comment. Depends on the in-class conversation we’ve already had about this issue.

Ben Lockeretz · August 4, 2016 at 10:06 pm

I would give full credit. It is not exactly a well-formed proof but I try to focus less on everything being written out just right and more on the fundamental reasoning. In this latest example it is very clear the student is manipulating one expression and getting the other. Lovely.
The original response discussed up above is a little shakier to me. It is true that ak = bk => a = b for k not 0 and by this fact the reasoning in the response works, but I’m not sure ak = bk => a = b counts as common knowledge that can go without stating. Does the student understand that their reasoning relies on that fact? Do they understand this is true for multiplication but not for instance squaring? Have they considered a 0 denominator? I have enough doubts I’d probably go with 1 point myself but if someone else at the grading table felt strongly it should get 2 I wouldn’t fight it.

MrHonner · August 5, 2016 at 9:38 am

The questions you have about the original response are reasonable, Ben, but I’m not sure we shouldn’t have similar, if not the same, questions about all of the other model responses that demonstrate full-credit work.

In one, a student writes a string of equivalent expressions with no equal sign; does that student understand that the application of transitivity requires equality? In another, a student replaces 1 with (x^3 + 8) / (x^3 +8); does that student understand this is only true as long as x <> 2 ?

The truth is, none of those responses provide any more justification than the response under scrutiny here. I’m not sure why we should hold this work to such a high standard and not the others.

Nick · August 6, 2016 at 11:44 am

“For the most part, there is no issue with multiplying both sides of a purported identity by the same quantity: if the original equation is true, the new equation will be true, and if the original equation is false, the new equation will be false.”

“For the most part” meaning it doesn’t constitute proof. Watch:

4=5
0*4=0*5
0=0

QED.

This method of proving A=B, where you start with A=B and do operatioms to both sides and end with C=C is not valid. You are assuming what you are trying to prove, as others have told you.

To prove A=B, you need to start with A=A, do some identity operations on the right hand side, and then end up with A=B.

Nick · August 6, 2016 at 11:48 am

Caveats: If you start witb A=B, and do only *invertible* operations to both sides and end up with C=C, you’re golden. This should be stated though, or alternatively you could just start with C=C and do operations to both sides and end with A=B. That would be proof.

John · January 11, 2017 at 5:10 pm

Okay, Patrick. I finally took your advice and wrote my own blog post on the subject of proving identities. Thanks for pushing me to do this! 🙂

https://mrchasemath.wordpress.com/2017/01/11/proving-identities-whats-your-philosophy/