Regents Recap — June 2016: Are These Figures Congruent?

Published by MrHonner on July 25, 2016July 25, 2016

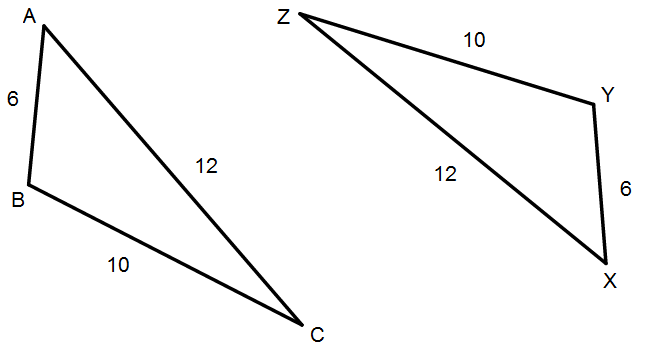
Given the congruent triangles below, is the statement “Triangle ABC can be proved congruent to triangle ZYX” true, or false?

I imagine most will say that the statement is false, and argue that the correspondence of the triangles is incorrect. That is, segment AB is not congruent to segment ZY, and so on. I think this is a reasonable response.

However, a substantial part of me believes the statement is true. “Triangle ABC” references an object, as does “triangle ZYX“. These two objects are indeed congruent. Thus, how can it be said they can’t be proved congruent?

In other words, I don’t believe the statement “Triangle ABC can be proved congruent to triangle ZYX” entails a binding correspondence in the way that the statement

$\Delta ABC \cong \Delta XYZ$

does.

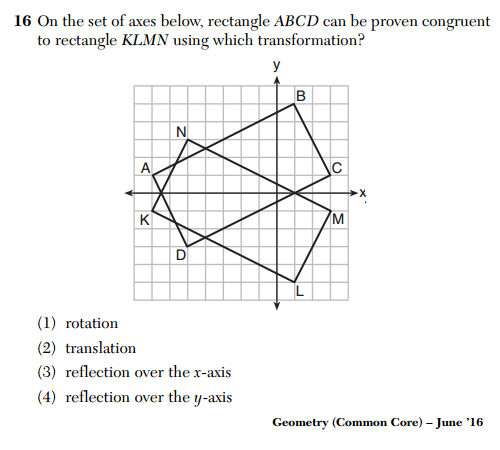
I was thinking about this because of this question from the June 2016 Common Core Geometry Regents exam.

According to the rubric, the correct answer is (3) reflection over the x-axis. The most common incorrect response, of course, was (1) rotation. But I’m not certain it’s really incorrect. I don’t think anyone would get this question wrong based on my objection, but since the question is designed to entice students to say rotation, I think it deserves some scrutiny.

Related Posts

Categories: GeometryTesting

15 Comments

Evelyn · July 25, 2016 at 3:45 pm

Yeah, I would probably have said rotation because it’s the first answer, and I can see a rotation that works.
Precision and attention to details are important in math, but to me rectangle KLMN is *the same object* as rectangle NMLK, and I agree with your “binding correspondence” point.
Even if you do believe in a binding correspondence, you could first prove that KLMN is congruent to NMLK using properties of rectangles and then do a rotation to prove congruence to ABCD.

Joshua · July 28, 2016 at 11:48 am

I strongly agree with your point, essentially poking at the phrasing “can be proven…using…”

Even requiring the binding correspondence, it is possible to write a proof showing congruence that uses, in a non-trivial way, any of those transformations.

This is a terrible question.

anon · July 25, 2016 at 7:16 pm

Yeah, I think this is another terrible one. It tests only one thing: knowledge of an ambiguous and arbitrary piece of notation/vocabulary.

Namely: does a rectangle come with a specific ordering of its points, and is congruence required to respect that ordering? To make an even more basic example than the one you led with: are the rectangles ABCD and BCDA in the picture congruent? Are the triangles ABC and BCA in your first picture congruent? I would say yes, but this test answer indicates no.

Of course, either one can be defended as a definition, and it would even be interesting to discuss this somewhat subtle point with students.

But without such a discussion it’s an arbitrary and irrelevant thing to base a question on.

Carl Oliver · July 25, 2016 at 10:26 pm

How is this false? The two triangles are congruent, they are testing whether the points listed in the notation correspond correctly, however poorly. How you choose to describe the triangle doesn’t change the fact that it is congruent or not, does it? Could you say that the statement “triangle XYZ could be proved congruent to triangle ZYX” is false?

MrHonner · July 26, 2016 at 7:43 am

I’m not sure I follow, Carl. It seems like you are both agreeing with me *and* defending the Regents question. So, for the Regents question, do you think Rotation is a correct or an incorrect response?

Carl Oliver · July 26, 2016 at 7:55 pm

For the first regents question, I really don’t know how you can say it’s false. But for the second question, rotation is a great answer. Maybe they intended to have “rotation about the origin” as the first answer which would have made reflection the only real choice, but they did not.

MrHonner · July 27, 2016 at 7:00 pm

Thanks for clarifying. For the record, the first question isn’t a Regents question: I made it up to get at the heart of matter with the actual Regents question.

Jim Doherty · July 26, 2016 at 9:29 am

A couple of points here regarding the triangle question. I admit that I did not look at the order of the naming of the triangle, I simply looked at the figures. This strikes me as the sort of distinction we routinely make that turns off people from mathematics. In other words, I agree with what you wrote that they are congruent figures and I feel okay about the answer I tweeted at you. However, the switch to using the congruence symbol and the order of vertices makes me feel guilty. I have almost certainly clucked at kids and reminded them that the order of the naming makes a difference. There is value to paying attention to this but it probably is overwhelmed by the perceived pickiness involved. I have had similar frustrations with proofs that distinguish between segment lengths being equal and segments being congruent. This sort of distinction probably does not help my students appreciate Geometry.
Now, on to the quadrilateral question. I have to imagine that you want to make a similar argument. That without the formal congruence symbol we can sort of wave away the order in which the figure is named. If I was grading this myself I would certainly accept rotation as an answer. However, mass graded tests are not programmed this way. So where does this leave us with our students?

MrHonner · July 26, 2016 at 6:31 pm

You raise an interesting point about how such technical distinctions can potentially turn people off from mathematics. At it’s heart, mathematics is a highly technical endeavor, but it’s important to show students that mathematics can be understood and applied both intuitively and rigorously.

Your example about segments and segment lengths is a good one. Personally, I make this distinction a consistent point of emphasis for my students, but my hope is that they understand it as a consequence of a fundamental property of mathematical objects (numbers can be equal, geometric figures can be congruent), not as a mere technicality.

Joshua · July 28, 2016 at 12:18 pm

In two situations (at the PROMYS program and my own HS geometry class), I’ve seen the following solution to this dilemma:
(1) an introductory phase where we focus on small, technical details, but the teacher emphasizes this, explicitly acknowledges that this is uncomfortable/artificial, but explains why it is useful and what we are learning through this pedantry. Here, the focus of a proof is tracing back the argument to the axioms and justifying every step.

During this phase, it can become a game to catch the teacher glossing over a technical point or skipping a step. Personally, I like empowering the students even farther and encouraging them to look for holes in the text, implicit assumptions in Euclid, etc.

Writing proofs in T-form can help visually reinforce the rules of play during this phase.

(2) A clear break where the rules are relaxed, where the focus proofs is now on clearly communicating the key insights, not every detail needs to be justified and not every technical point needs made explicit (especially segments vs segment lengths!)

Of course, there is still a tension about what is enough, too much, or not enough detail. Some “proofs” of false results come in handy here show what can go wrong.

In both cases, the rules on the exam were also made clear. Unfortunately, I wouldn’t know how to fit this approach into a standardized exam.

Jacob M · July 26, 2016 at 12:25 pm

I think the Regents question hints at a pretty interesting problem as to what a rectangle (triangle, polygon) ‘is’. More specifically, when we specify one, does it include a prescribed orientation? It’s it’s pretty easy to reason no. The above triangles should be congruent in that case, and the rectangles would be congruent by rotation as well as reflection.

We could also make an argument however that polygons should come with orientations. This too isn’t an unreasonable way to look at it – when doing a contour integral around a loop, we need to specify an orientation. It was once explained to me in the following way. We want the area of a triangle to be a smooth function of its coordinates. We can imagine shrinking one side of a given triangle until we have a line, and then continuing this motion, so that we have essentially reflected the triangle across one of its sides. Since this motion was smooth, the area should behave smooth, or after reaching zero area, should continue decreasing to being negative. So even though the resulting triangle has the same side lengths, it has a different area and so can’t be ‘the same triangle’. This negative area corresponds to a difference in orientation.

In that case the two triangles above wouldn’t be congruent (as they have different orientations). I’m not sure we could say that the two rectangles in the regents problem are congruent per say, but the mapping which gets us the correct orientation would be a reflection, not a rotation.

That being said, this justification was based on ambiguity, and the question is rather misleading.

MrHonner · July 26, 2016 at 6:20 pm

I’ve never heard that explanation of orientation as a means to make area a smooth function of the coordinates. That’s lovely! Thanks for sharing, Jacob.

Some mathematicians have also made remarks about orientation on my Google+ post. You might be interested in checking them out: https://plus.google.com/u/0/+PatrickHonner/posts/N8ZpsA21FPk

Jonathan Halabi · July 26, 2016 at 7:42 pm

That orientation thing – big deal – for PROVING triangles congruent (think SAS vs SSA), but I agree, congruent triangles are congruent triangles, they are complete objects, independent of labeling.

I think this is a case of repeating what we got from the book – when we were students. Shame that so many of us use our knowledge of high school geometry, and nothing beyond, to teach high school geometry (and to write state exams)

Jim Doherty · July 26, 2016 at 8:17 pm

Interesting that you point out these two congruence defenses. Given that the triangles are congruent, a fact obvious to many/most of our students, might render the REASON for defending their congruence pretty uninteresting to our students. These are powerful theorems for proving things congruent when it is not inherently obvious that they are. In this case, we know the congruence at a glance.

Jonathan Halabi · July 26, 2016 at 9:31 pm

I point out those two as beginning geometry students sometimes confuse SAS (which generally shows congruence and is treated as a theorem) with SSA (which shows congruence if we already know both triangles are obtuse, or both are acute, but is not generally treated as a theorem). Listing the parts in order can help differentiate the two cases.

Of course, it’s usually obvious when a scale diagram is included.

Jonathan