Regents Recap — June 2015: Are They Reading?
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
I have been reviewing New York State Math Regents exams for several years now, and I occasionally wonder if anyone involved in the production of the exams pays attention to what I say.
Earlier this year I wrote about a terrible question asking students to justify why the sum of a rational number and an irrational number is irrational. (Answer: because the sum of a rational number and an irrational number is always irrational.)
So I was pleasantly surprised to see this question in the June 2015 Common Core Algebra exam.
This multiple choice question assesses the same concept, but doesn’t ask the student to write a circular explanation as justification. The less these tests ask students to do mathematically meaningless things, the better.
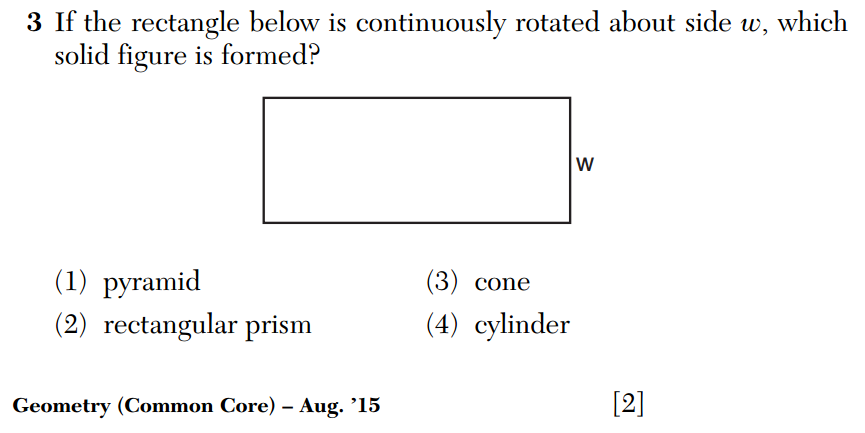
I also had serious complaints about how certain 3D geometry concepts were handled on the June, 2015 Common Core Geometry exam. In particular, a solid of revolution problem was very poorly stated. This question from the August, 2015 Common Core Geometry Regents exam shows some improvement.
It’s also true that recent locus questions have not suffered from the imprecise language I complained about some time ago: in the last few iterations, problems have been more carefully worded to ask students explicitly to sketch individual loci and then indicate their intersection.
In the vastness of these flawed tests, it’s nice to occasionally see some progress.

1 Comment
David Richeson · September 1, 2015 at 9:37 am
The rational/irrational question is certainly much better than the one you link to, but I still would not word the question in that way. The four sentences given below the question are logical statements, and statements are either true or false—there’s no “always true” in logic. It is just “true.” If it isn’t “always true,” then it is false. In this case statements 1, 3, and 4 are true, 3 is false. Option 3 is really saying “For all irrational numbers a and b, ab is rational” or “For all real numbers a and b, if a and b are irrational, then ab is rational,” which is false. (I know what they are saying. They’re saying to consider the predicate “If a and b are irrational numbers, then ab is rational.” Then their question is “Is this predicate true for all real numbers a and b?” The answer is no.) In short, if I were to give this question in our Discrete Math class (in which we talk about topics like this) I would ask “Which statement is false?” The answer is 3 and a counterexample is a=1, b=sqrt(2).