An Impossible Construction
I enjoy offering impossible problems to students as extra credit, although I usually don’t tell them the problems are impossible. Such tasks usually engage them, confuse them, and make them suspicious of me. It’s a win-win-win.
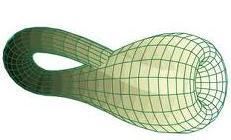
While discussing some three-dimensional geometry, I offered extra credit to anyone who could build a model of a Klein bottle. The Klein bottle is a hard-to-imagine surface that has neither an inside nor an outside. It’s like a tube where one end meets the other and makes a seal, but somehow got turned inside out in the process. If you are familiar with the Mobius strip, the Klein bottle is basically a higher-dimensional Mobius strip.
One reason that the Klein bottle is hard to visualize is that it can’t be observed in three dimensions: it needs a fourth dimension in order to see it turn itself inside-out. This is analogous to the standard construction of the Mobius strip: we take a long strip of paper, give one end a half-twist, and tape the ends together. We think of the paper itself as being 2-dimensional, but we need that third dimension to twist through.
So, I was pretty impressed with the student who made this.

Not bad at all, for someone who is dimensionally challenged. Here’s a nice representation for comparison, although it’s still a cheat. The Klein bottle doesn’t really intersect itself.
A nice example of impossibly creative student work!
0 Comments