Search Results for: workshop

Workshop: Session 6 — Summary

We began by looking at some of the lovely mathematics of infinite series. Working with the geometric series

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \ldots$

we explored partial sums, the formula for the sum of an infinite geometric series, and some ideas in Calculus.

By looking at the partial sums of this series, a lot of good ideas surface:

$\frac{1}{2}=\frac{1}{2}$

$\frac{1}{2} + \frac{1}{4}=\frac{3}{4}$

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8}=\frac{7}{8}$

You can quickly generalize to the formula

$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \ldots + \frac{1}{2^n} = \frac{2^n-1}{2^n}$

With this, you can predict the answer (1!) and discuss ideas like limits.

Still working with the above series, you can explore the way in which we derive the formula for the sum of an infinite gepmetric series.

Take the original series, set it equal to S

$\qquad\quad \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \ldots = S$ (Eq 1)

multiply this equation by 2

$2( \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \ldots = S)$

to get

$1 + \frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \frac{1}{16} + \ldots = 2S$ (Eq 2)

Then subtract Eq1 from Eq2 to get the magical result

$S = 1$

A nice geometric interpretation of this can be seen in this Proof Without Words.

The same approach produces the general formula for the sum of infinite geometric series:

$a + ar + ar^2 + ar^3 + ar^4 + \ldots = \frac{a}{1-r}$

We also had some fun looking at series where r, the common ratio, didn’t satisfy the requirement $|r| < 1$ .

Click here to return to CMT Workshop Homepage.

By patrick honner, 14 years12 years ago

Workshop: Session 5 — Summary

Before we started talking about sequences, we looked another folding problem involving medial triangles.

We started talking about some fun sequences, and we found the next terms for most of them. Hopefully no one lost too much sleep over the tricky ones!

We talked a bit about the method of finite differences for finding an n-th term formula for a given sequences. For example, by looking at the difference of consecutive terms

we see that it takes two iterations to get to a constant difference. This means that nth term of the original sequence is quadratic! Naturally, we recognize the original sequence

as triangle numbers, and the formula for the nth triangle number is well known to be $\frac {n(n+1)}{2}$ , a quadratic function.

We also looked at some ways to use the method of finite differences backwards, that is, to find the sum of sequence, i.e. a series. For instance, if we wanted to find the sum of the triangle numbers, we could work up like this

and get the tetrahedral numbers (the sequence in red), whose formula is well-known to be cubic.

In the second half, we looked at several activities that use Excel to explore sequences and series. In particular, two of the activities I showed you were taken directly from these videos on Excel and Pascal’s Triangle and Excel and Fibonacci Numbers.

Last, we talked a little about the Purple Comet contest, which is going on now! Get a team together, sign them up, and have fun!

Click here to return to CMT Workshop Homepage.

www.MrHonner.com

By patrick honner, 14 years12 years ago

CMT Workshop on Extracurricular Mathematics

Led by Patrick Honner, Brooklyn Technical High School and Mark Saul, PhD, Center for Mathematical Talent.

Sponsored by the Center for Mathematical Talent (CMT) at the Courant Institute of NYU.

Session Summaries

Session 1: Counting Rectangles

Session 2: Pythagorean Theorem

Session 3: Counting Subsets

Session 4: Connecting Midpoints

Session 5: Sequences and Series

Session 6: Infinite Series

Addenda

Participant Presentations

Some Technology Ideas for Inside and Outside the Classroom

Fun With Folding

Thanks for a great workshop!

www.MrHonner.com

By patrick honner, 14 years ago

Workshop: Session 4 — Summary

We began by looking at three proofs of one of my favorite theorems in geometry: the line segment connecting the midpoints of two sides of a triangle is parallel to, and half the length of, the third side.

Proof 1 was the “textbook” proof involving the Side-Angle-Side Similarity Theorem: prove the small triangle is similar to the large one by SASS. Congruent corresponding angles give you parallel lines and proportions gives you the length.

Proof 2 is one of the reasons I love this theorem so much: I use it as a transition back to coordinate geometry. There is certainly a lot of background work hiding in the shadows (the distance and midpoint formulas; tying slopes to parallelism and perpendicularity; establishing what arbitrary figures really are), but a few simple calculations give you both the length and the parallelism.

Before really using coordinate geometry to prove theorems, however, make sure you fully explore the idea of an arbitrary figure. Ask students to sketch and label an arbitrary quadrilateral in the xy-plane: if a square, rectangle, trapezoid, or kite comes back, try again!

Proof 3 is an elegant proof shown to me by a student. Just rotate the triangle 180 degrees around the midpoint!

Just convince yourself that M, N, and M’ are all collinear and that CABA’ is a parallelogram, and you’re done!

As an extension of this idea, we discussed Varignon’s Theorem: take any quadrilateral, connect the midpoints of adjacent sides and a parallelogram is formed! Even more amazing is that this theorem holds for concave and even complex quadrilaterals!

This is a great activity for paper-and-pencil exploration, or with dynamic geometry software like Geogebra.

We also talked about a lovely problem from the 2011 AIME that incorporated a similar idea, namely, taking a scalene triangle and bending the corners down to make a table.

Click here to return to CMT Workshop Homepage.

By patrick honner, 14 years9 years ago

Workshop: Session 3 — Summary

We began by looking at some approaches to the “How many subsets?” problem.

Listing out all of the subsets is a great way for students to get their hands dirty, and it allows for various patterns to emerge from the lists.

Here we have categorized the subsets in a natural way, by size. (Note: you can always have fun by arguing whether or not the empty set should count!). Lots of great symmetry here in this diagram, and patterns to explore. In particular, this is a great way to illustrate two fundamental principles of combinatorics.

First, ${_n}C_r$ is the number of ways to choose r things from n, so it makes sense that this number is the number of subsets of size r: to make a subset of size r from a set of size n, you need to really choose r of the n available things.

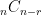Furthermore, the various lists illustrate the relationship between ${_n}C_r$ and ${_n}C_{n-r}$ . How do you make a subset of size 1? Pick one of the elements from the five. But notice that what’s left over is a subset of size 4! Thus, for every way you can take one thing from five, there is a corresponding way to take four things from five.

Another great way to illustrate this is with a group of five students standing in front of the class. Pull one aside: did you make a group of one? Or a group of four?

Lastly, this problem provides a great opportunity to change your perspective. Instead of counting the subsets by size, think of naming every subset as a word consisting of Ys and Ns. Each letter of the word corresponds to a particular element of the set; Y means “Yes, you are in the subset”, and N means “No, you are not in the subset”. Here are some examples:

Every subset can be uniquely identified in this manner, and the beauty of this approach is that it is easy to count how many five-letter words there are of Ys and Ns: it’s just ${2^5}$ .

Not only is this a great way to illustrate the changing your perspective strategy, but you can also explore the basic idea of a combinatorial argument. In essence, we have counted the same thing (the number of subsets) in two different ways; thus, the ways must be equal! This basic idea gives us one of the fundamental combinatorial identities:

In the second half of the session we played around with a Mandelbrot Team contest on binary numbers. At the Mandelbrot Contest website, you can look at some sample contests (both individual and team), order books of past contests, and register for the official contests.

The individual Mandelbrot contests are usually pretty challenging, but they contain great problems, and the team contests are wonderful. The Mandelbrot Team contest takes a rich mathematical problem and breaks it down into 5 or 6 interconnected parts that range from simple exploration to sophisticated abstraction. These are a great way to build team dynamics in your classes, and a great model for constructing your own guided learning activities, too!

While working through the contest, we had some fun exploring binary representations, binary addition, and binary fractions! Larry showed us a cool way to find a numbers binary representation: the upside-down division method shown here. And he also showed us a fun way to convert fractions into binary by repeated multiplication by 2.

Click here to return to CMT Workshop Homepage.

www.MrHonner.com

By patrick honner, 14 years ago