While cleaning up after a successful group build, a colleague and some students had fun making a little Thanksgiving tribute in Zometool.
Resources Teaching Technology
Derivatives of Vector Functions
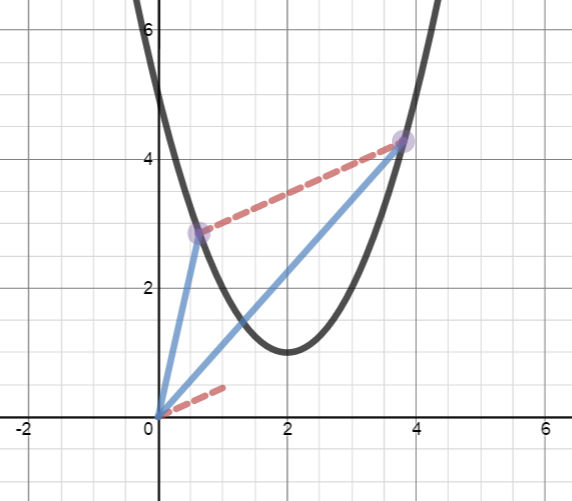One way to think of a curve in the plane (or in space) is as a collection of terminal points of vectors whose initial points are all at the origin. The vectors are given by a vector-valued function.
For example, the parabola shown at right can be thought of as the graph of the vector-valued function
I’ve created a Desmos demonstration that shows how graphs of vector-valued functions are related to their vectors (shown in blue), and how the derivative of a vector-valued function is related to both difference vectors and tangent vectors. You can access the demonstration here.
You can find more of my Desmos demonstrations here.
Appreciation Geometry Photography
Math Photo: Undersea Rose Curve
I can’t look at this lovely jellyfish without seeing a four-petal rose curve in the polar plane.
NYT Resources Teaching
Exponentials and Ebola
My latest piece for the New York Times Learning Network is a lesson on the underlying mathematics of the spread of contagious diseases, like Ebola.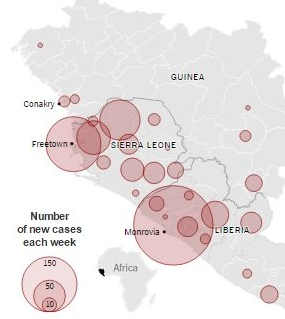
In this lesson, students use a basic exponential model to explore the fundamental mathematical ideas of transmission and replication.
Mathematically, the spread of disease can be modeled in a manner similar to the spread of a rumor. Although a number of simplifying assumptions must be made, the simple exponential model captures the basic impact of transmission rates on the dispersion of a disease among a population. Students can explore the consequences of transmission rate using multiplication, algebra, graphing utilities and elementary statistics.
After exploring the essential behavior of various simple exponential models, students then compare real-world data to their theoretical models. Those that are capable can perform regressions on the data to approximate actual transmission rates. The students’ work and the real-world data establish a context for discussing the strengths and weaknesses of this simple model of disease transmission.
This lesson is part of a series of Ebloa lessons at the NYT Learning Network and is freely available here.
Art Teaching Technology
Math Art: Twilight on Mars
I was playing around in Scratch this weekend, experimenting with some numerical methods for approximating integrals, when this lovely image unexpectedly emerged. I call it Twilight on Mars.
Twilight on Mars
Looks like I’ve got a new math and art project for students, and me, to explore!