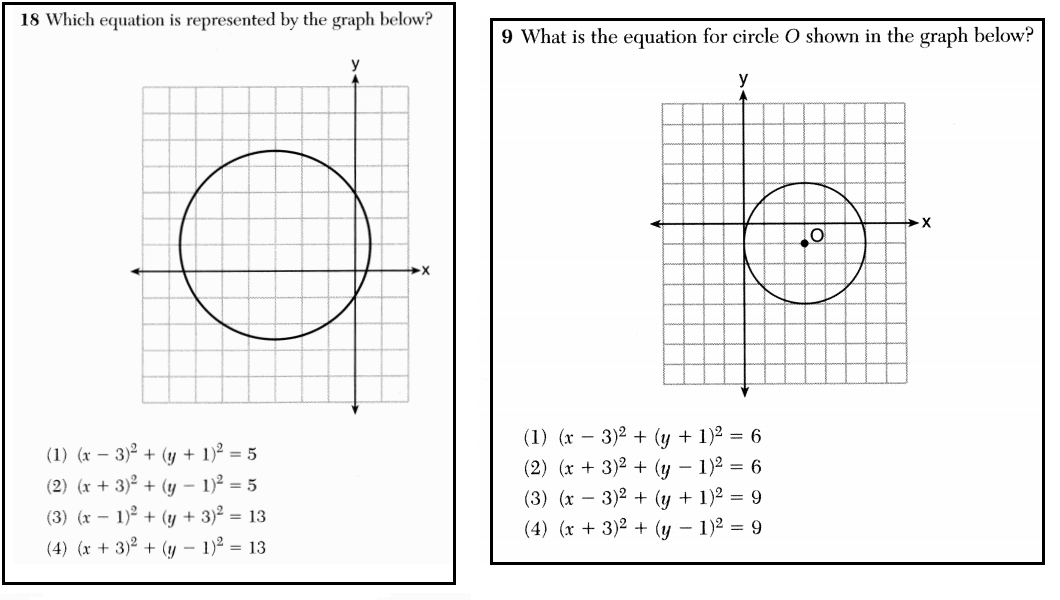
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
Here are two questions from the June 2013 exams.
These questions aren’t particularly interesting: both give the graph of a circle and ask for its equation. Since the questions are nearly identical, it would be strange to see them on the same exam. It is even stranger, then, to see them on two different exams: one was on the Geometry exam, the other the Algebra 2 / Trig exam.
Why does the same kind of question appear on the terminal exams of two different, sequential courses? Are students supposed to learn this topic in Geometry, or in Algebra 2 / Trig? The test-makers don’t seem to know, which calls into question the fairness of these exams.
And the question of fairness has implications for teachers as well as students. Student exam scores now constitute a substantial component of a teacher’s yearly evaluation. If students are supposed to learn how to find the equation of a circle in Geometry class, is it fair to use such a question to evaluate an Algebra 2 / Trig teacher?
The fact that test-makers don’t know which topics belong in which courses raises some serious questions about the validity of using these test results to evaluate teacher performance. In addition, one wonders how facing the same question on sequential exams impacts student growth measurements so popular among educational policymakers nowadays.
Unfortunately, this is only the latest in a long line of inappropriate questions on math Regents exams.