July 2013

Here is another installment in my series reviewing the NY State Regents exams in mathematics.

Consider the following three questions from the June 2013 New York math Regents exams.

From top to bottom, these questions appeared on the Integrated Algebra exam, the Geometry exam, and the Algebra 2 / Trig exam.

Solving systems of equations is a fundamental mathematical skill and should be a part of any math course.  But do these three questions really span 3-4 years of mathematical learning?

The first two are simply different representations of the same problem.  The third question involves a relation instead of a function, but it’s presentation as a multiple choice question sidesteps any additional algebraic or geometric complexity that dealing with a relation might entail.  Ironically I think the question from the earliest exam is the hardest of the three.

I’ve written about this curious treatment of systems of equations in analyzing other Regents exams.  This phenomenon comes to mind when politicians and administrators take credit for raising test scores, or trumpet gains in student growth from year-to-year.

As part of my ongoing series reviewing the NY State Regents exams in mathematics, I recently wrote about mathematically erroneous questions in the June 2013 exams.

In the original post I took issue with number 25 from the Algebra 2 / Trig Regents exam.

I complained that the denominator here can’t really be “rationalized” since it is a variable expression.  This complaint was thoughtfully refuted by a commenter who pointed out that I was thinking of the process of “rationalizing” as applying only to numbers.  The process can be interpreted to apply to functions, and while I personally don’t like this use of the term, it does appear as a standard in the Alg 2 / Trig course.  As a result, I withdrew my criticism and updated the post.

Ironically, the commenter’s thoughtful and informed refutation actually pointed to a different reason this question is mathematically erroneous.  [This emphasis here is mine.]

Admittedly, they never specify whether this expression is meant to represent a function of x or a specific number. They certainly intended the former, since they say the answer is (1) rather than (4): technically, (1) and (4) define slightly different functions (since 0 is in the domain of (4) but not (1)),while if you interpreted the original problem as a number, then (1) and (4) would define exactly the same number as you started with.

If we are talking about functions, then although (1) and (4) both appear to be equivalent to , only (1) is truly equivalent since only (1) has the same domain (, ) as the original.  The commenter argues that declaring (1) and not (4) to be the correct answer is evidence that the test-makers intended the question to be about rationalizing functions, and that they understand the mathematics of the situation.

This is an excellent point.  As it turns out, however, I had mistakenly reported that (1) was the official correct answer.  In fact, (4) is the official correct answer, despite the fact that it is not equivalent to the original expression (which, unlike (4), is undefined for ).  Incidentally, this lack of understanding of equivalent expressions is consistently demonstrated on these exams.

Presumably, the requirement that the answer be in simplest form is what makes (4) and not (1) correct in the minds of the test-makers.  But cancelling out common variable factors doesn’t just simplify expressions–it changes them by altering their apparent domains.   And to me, simplest form is a characteristic of numbers only, not of expressions, which further clouds the issue of what the authors intended here.

A follow-up question might help clarify the mathematical thinking here:  how would one express  with a rational denominator and in simplest form?

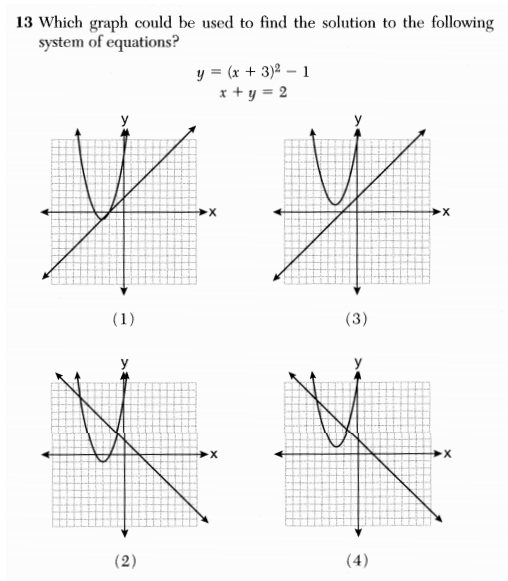
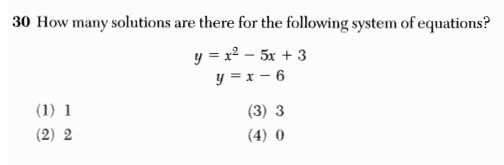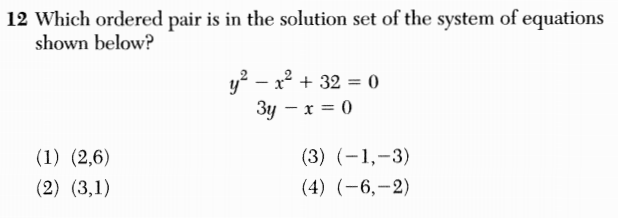Here is another installment in my series reviewing the NY State Regents exams in mathematics.

It’s probably unavoidable that large-scale standardized exams will contain errors.  But some errors are more serious than others.

The New York math Regents exams consistently contain errors that demonstrate a lack of mathematical understanding on the part of the test-makers.  These aren’t just “typos”, as administrators and politicians often suggest;  they are serious conceptual errors, and they call into question the validity of these assessments.

Consider number 24 from the Geometry exam demonstrates several different kinds of errors.

The test-makers indicated that (2) is the correct answer.  Presumably, they believe the acronym SAS stands for the Side-Angle-Side Similarity Theorem.  However, SAS typically stands for the Side-Angle-Side Congruence Theorem.  If a student interpreted SAS, SSS, and ASA in the usual way, i.e. as congruence theorems, then AA would be the only possible way to prove two (non-congruent) triangles similar, and thus (1) would be the correct answer.

Perhaps the test-makers might claim that the context of the problem, proving similarity, should have led students to assume the acronyms stood for similarity theorems.  But, alas, there is no ASA similarity theorem.  What were they thinking here?

More generally, “Which method could be used” is not a good mathematical question.  Lots of different methods could be used.  It’s not inconceivable that AA could be used to prove these triangle are similar, so how could that possibly be an incorrect answer to this question?  Ultimately this question was thrown out, but not before thousands of students across the state had already taken their final exam.  And even as they tossed the problem out, the state still refused to accept responsibility for publishing an erroneous question, hiding behind the old alternative methods defense:

Since there are alternative methods to prove that the two triangles given in Question 24 are similar, all students should be awarded credit for this question. (link)

Unfortunately, this is just the latest example of serious mathematical errors in NY State Regents exams.

[Update:  An earlier version of this post criticized #25 on the Algebra 2 / Trig Exam.  Thoughtful comments provoked me to re-examine my criticism, and also pointed to a different issue with this question, which can be found in a separate post.]