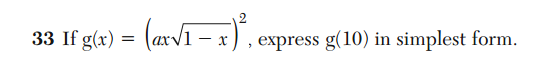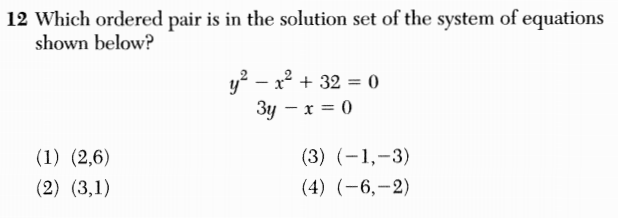Here is another installment in my series reviewing the NY State Regents exams in mathematics.
Functions seem to be an especially challenging topic for the writers of the New York State math Regents exams. After this debacle with functions and their inverses, we might expect closer attention to detail when it comes to functions and their domains and ranges. We don’t seem to be getting it.
Consider this question from the June 2013 Algebra 2 / Trig exam.
According to the rubric, the correct answer is . This indicates that the test-makers either (a) don’t understand the concept of domain or (b) they have decided to start working in the world of complex-valued functions without telling the rest of us.
Let and
, and note that
. In order to evaluate
, we first have to evaluate
. But
, which isn’t a real number. Thus
is undefined; in other words, 10 is not in the domain of
.
But if 10 is not in the domain of , it can’t be in the domain of
either. Therefore,
is undefined; it is not
, as indicated in the rubric.
Of course, if we are working in the world of complex numbers, . But we never talk about complex-valued functions in Algebra 2 / Trig. When we talk about functions like
, we are always talking about real-valued functions. And just because the process of squaring later on down the line eliminates the imaginary part, that doesn’t fix the inherent domain problem. After all, what is the domain of
?
What are the test-makers thinking here? I really don’t know.
Related Posts
- Regents Recaps
- The Worst Regents Question of All Time?
- Another Embarrassingly Bad Math Exam Question
- Regents Recap — June 2016: Algebra is Hard