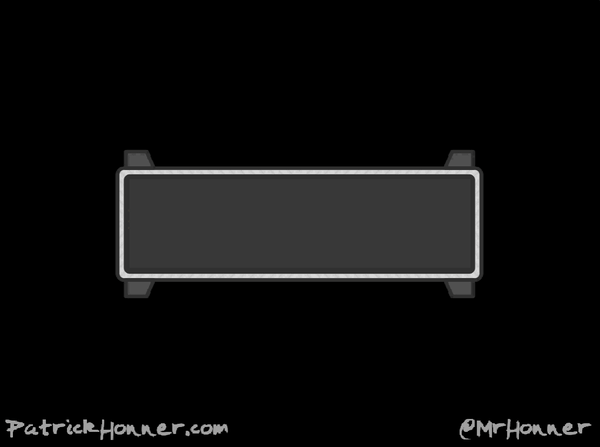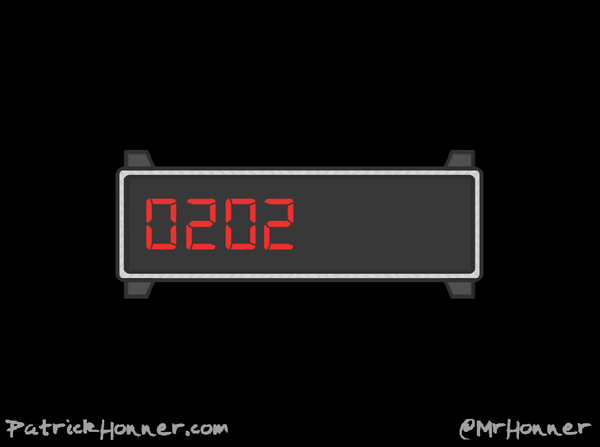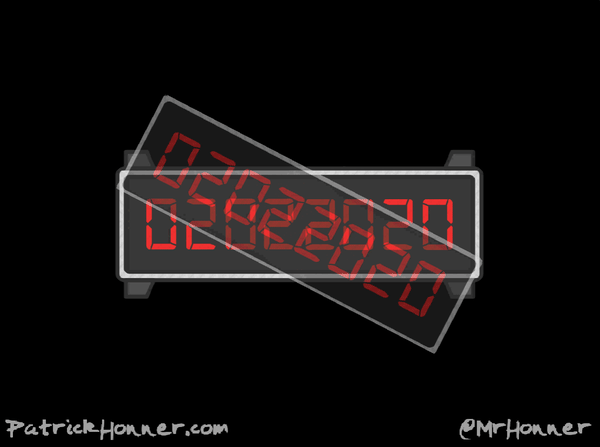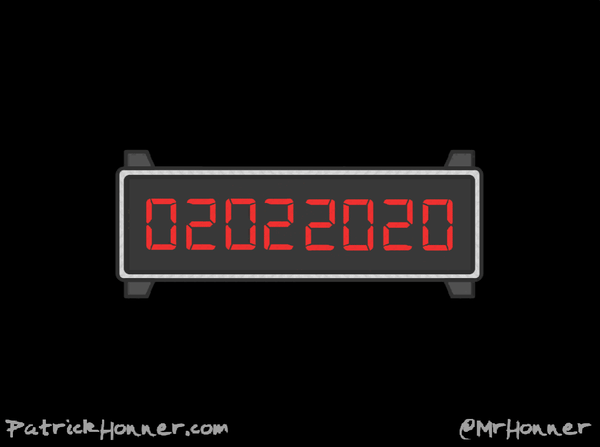
Here’s my tribute to today’s date: a palindrome with rotational symmetry!
Related Posts
Today we celebrate a Permutation Day! I call days like today permutation days because the digits of the day and the month can be rearranged to form the year.
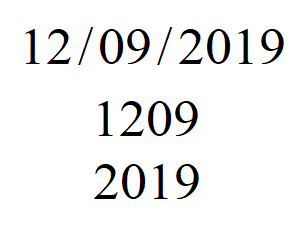
Celebrate Permutation Day by mixing things up! Try doing things in a different order today. Just remember, for some operations, order definitely matters!
My latest column for Quanta Magazine is about the search for sums of cubes. While most integers are neither cubes nor the sum of two cubes, it is conjectured that most numbers can be written as the sum of three cubes. Finding those three cubes, however, can be a challenge.
For example, it was only this year we learned that the number 33 could be written as a sum of three cubes:
33 = 8,866,128,975,287,528³ + (−8,778,405,442,862,239)³ + (−2,736,111,468,807,040)³
What’s so hard about expressing numbers as a sum of three cubes?
It’s not hard to see that it combines the limited choices of the sum-of-squares problem with the infinite search space of the sum-of-integers problem. As with the squares, not every number is a cube. We can use numbers like 1 = 1³, 8 = 2³ and 125 = 5³, but we can never use 2, 3, 4, 10, 108 or most other numbers. But unlike squares, perfect cubes can be negative — for example, (-2)³ = -8, and (-4)³ = -64 — which means we can decrease our sum if we need to. This access to negative numbers gives us unlimited options for our sum, meaning that our search space, as in the sum-of-integers problem, is unbounded.
To learn more, read the full article, which is freely available here.

Today we celebrate a Permutation Day! I call days like today permutation days because the digits of the day and the month can be rearranged to form the year.
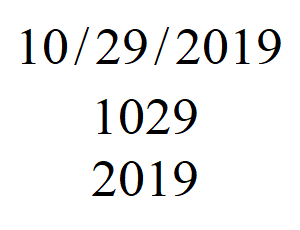
Celebrate Permutation Day by mixing things up! Try doing things in a different order today. Just remember, for some operations, order definitely matters!
Did you get caught up in the latest viral math problem, 8÷2(2+2)?
The problem here is simply how we interpret the division symbol. Does ÷ mean divide by the one number right after it or by everything after it? This isn’t much of a concern for most mathematicians, as they don’t use this symbol very often. Ask them to solve this problem and they’ll probably just make the whole thing into a multiplication problem: Once you choose to write it as either
or
,
the ambiguity is gone and the answer is clear. As a multiplication question, this isn’t particularly interesting.
But one multiplication question mathematicians do find interesting may surprise you: What is the best way to multiply?
And what is the best way to multiply? The answer may surprise you! Find out by reading my latest column for Quanta Magazine, freely available here.
