I’d never looked closely at the Parachute Jump in Coney Island, but recently noticed the octagons at each vertex of the dodecagon 250 feet up in the sky. It really is a beautiful structure, but I’ll leave it up to you to decide whether or not it deserves to be called “the Eiffel Tower of Brooklyn”.
Related Posts
Varignon’s Theorem is one of my favorite results in elementary geometry: connect the adjacent midpoints of the four sides of any quadrilateral, and a parallelogram is formed! It is a magical result that defies expectations, and it’s so much fun to play around with, explore, and extend.
Steven Strogatz shared his favorite proof of Varignon’s Theorem on Twitter yesterday, and so I felt compelled to share mine. This is a standard proof of Varignon, but it is so clean and elegant: it is an immediate consequence of the Triangle Midsegment Theorem and the transitivity of parallelism.
Strogatz’s vector proof is beautiful and efficient, but the power of transitivity really shines in this elementary geometric proof.
I created a a simple Desmos demonstration to explore Varignon’s Theorem. And like all compelling mathematical results, there are so many fascinating follow-up questions to ask!
Related Posts
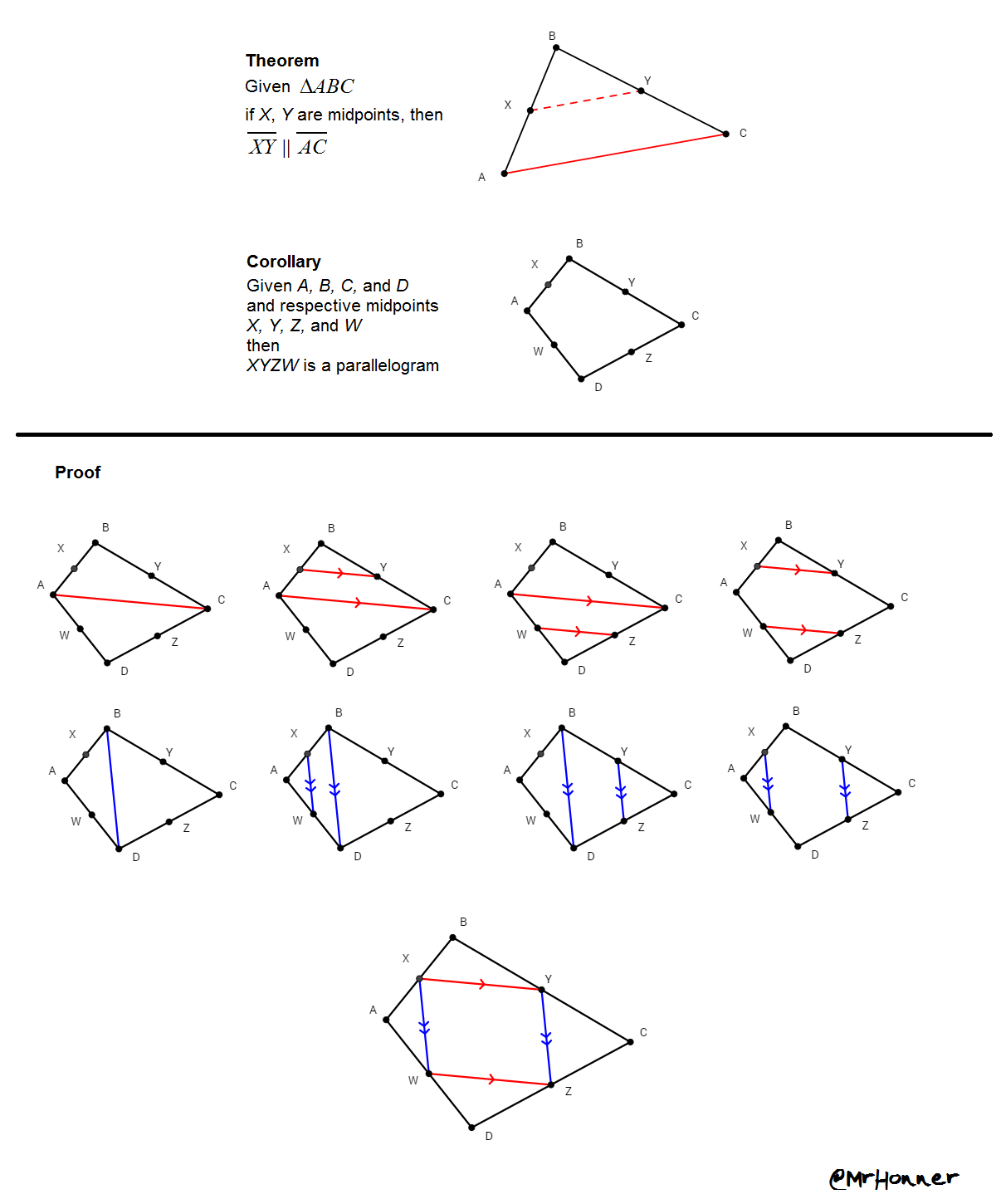
Given the congruent triangles below, is the statement “Triangle ABC can be proved congruent to triangle ZYX” true, or false?
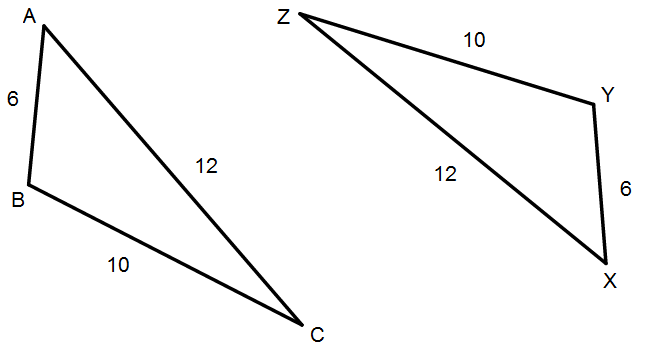
I imagine most will say that the statement is false, and argue that the correspondence of the triangles is incorrect. That is, segment AB is not congruent to segment ZY, and so on. I think this is a reasonable response.
However, a substantial part of me believes the statement is true. “Triangle ABC” references an object, as does “triangle ZYX“. These two objects are indeed congruent. Thus, how can it be said they can’t be proved congruent?
In other words, I don’t believe the statement “Triangle ABC can be proved congruent to triangle ZYX” entails a binding correspondence in the way that the statement
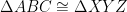
does.
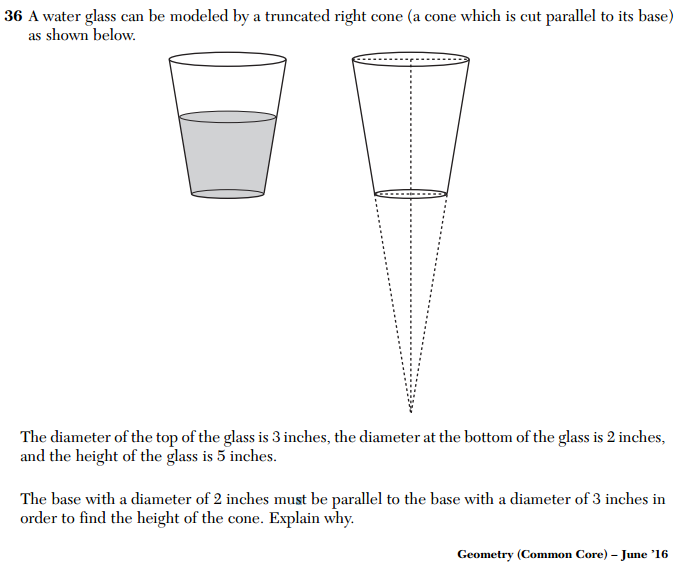
I was thinking about this because of this question from the June 2016 Common Core Geometry Regents exam.
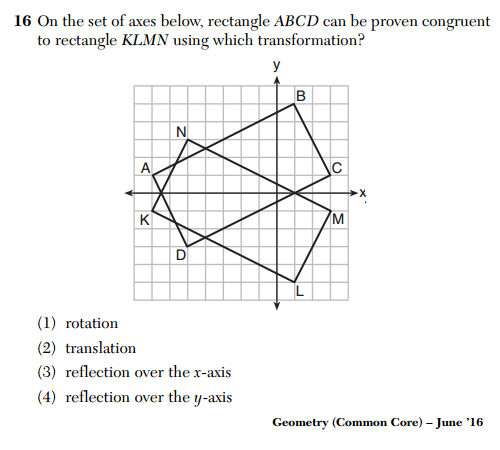
According to the rubric, the correct answer is (3) reflection over the x-axis. The most common incorrect response, of course, was (1) rotation. But I’m not certain it’s really incorrect. I don’t think anyone would get this question wrong based on my objection, but since the question is designed to entice students to say rotation, I think it deserves some scrutiny.
Related Posts
I read this problem several times and still did not understand what it was asking for. It is the first part of problem 36 from the June 2016 Common Core Geometry Regents exam.
“The base with a diameter of 2 inches must be parallel to the base with a diameter of 3 inches in order to find the height of the cone. Explain why.” Explain why? What do they want to hear?
Is the expectation that students will say something like “Height is only well-defined when measured between two parallel objects”, or “If the bases aren’t parallel, the height will vary depending on where the measurement is taken, thus height is only a meaningful measurement when the bases are parallel”? As usual, the rubric was no help, simply awarding points if A correct explanation is given.
But the model student work says it all. Here are two examples of complete and correct solutions.
These are not explanations of why the two bases must be parallel. These are descriptions of how you might compute the height given that the two bases are parallel. This argument essentially says “The bases are parallel because in order answer this question I need to apply a technique that requires that the bases be parallel.”
Not only is this not an explanation, it’s a kind of argument we want to teach students not to make. Validating these responses works against what we should be trying to do as math teachers.
These high stakes exams shouldn’t encourage teachers to promote invalid mathematical thinking. Unfortunately, as the posts below suggest, it’s happening far too often.
Related Posts
A new favorite building, on the West side. The strategic use and placement of non-congruent rectangles produces a pleasing result.
