An example of tiling the plane with regular hexagons. Well, maybe not the whole plane, but you get the idea.
A valid tiling of the plane means that everything fits together perfectly–no gaps.
A nice simple little exercise is trying to figure out which regular polygons can be used to tile the plane like this. The next step is to allow the use of more than one kind of regular pentagon, and so on.
There must be a good geometry problem in here somewhere.
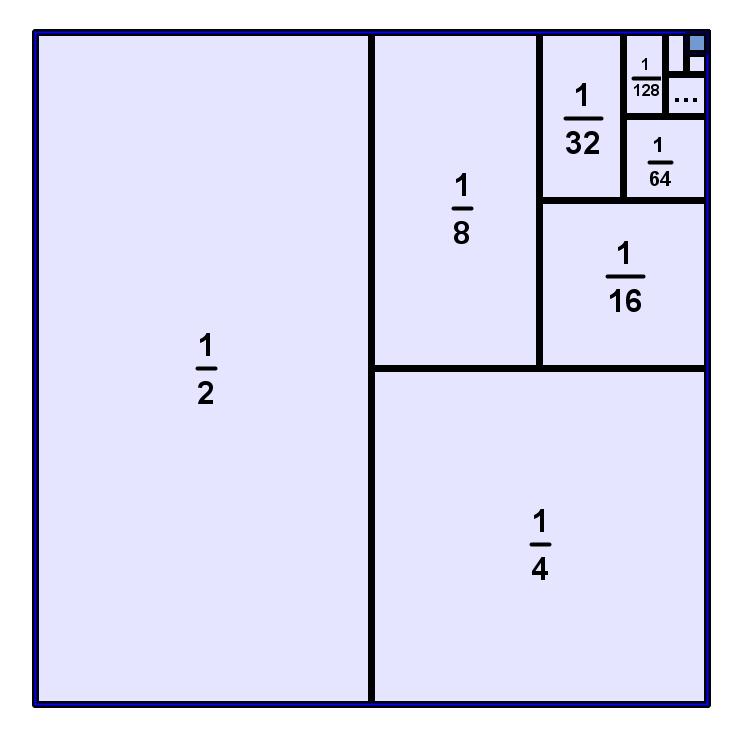
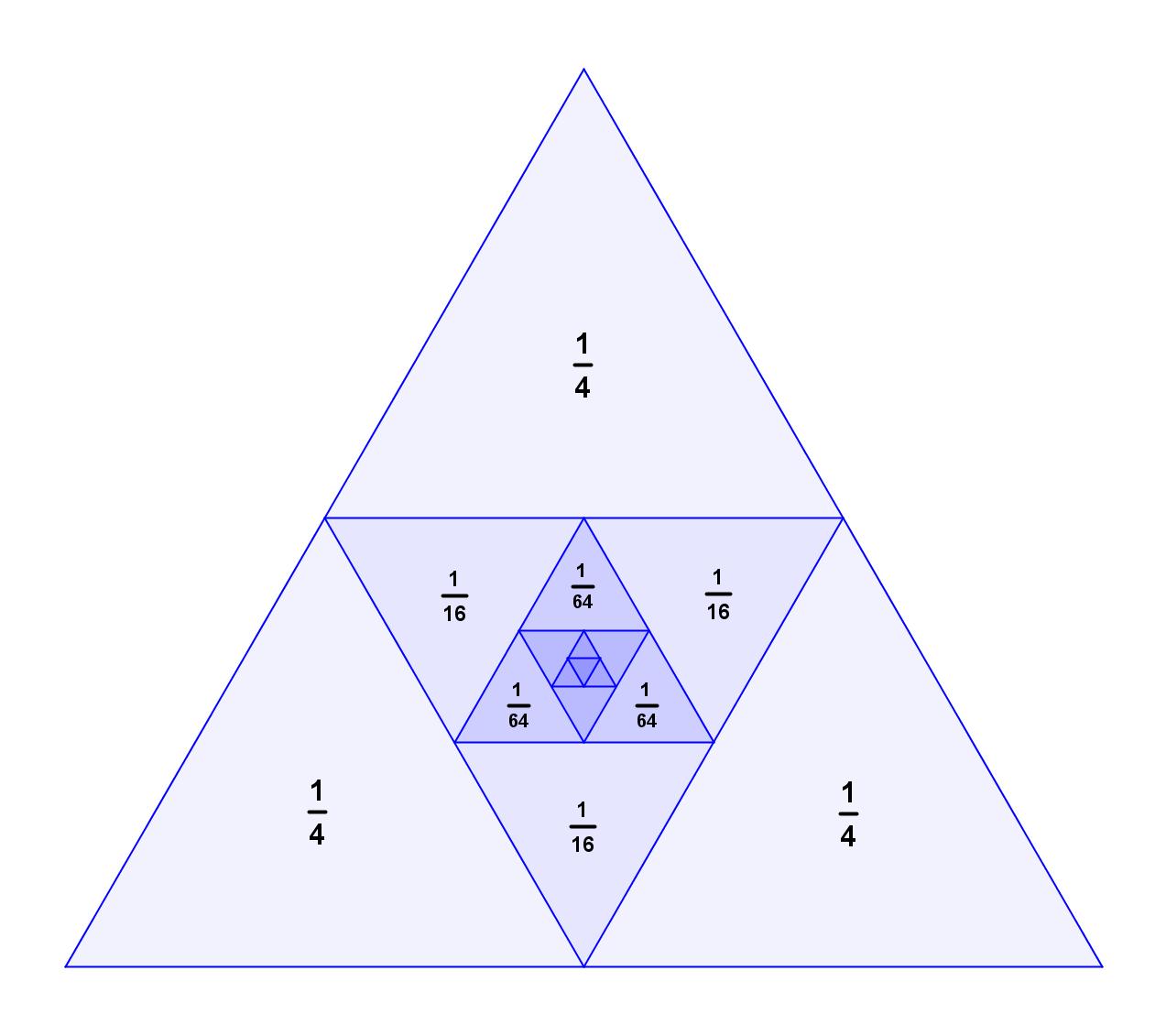
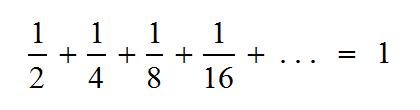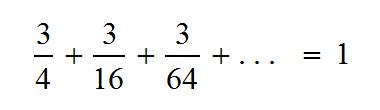I recently attended a function at the Museum of Modern Art hosted by Math for America. In typical MfA fashion, the invitation was designed around a relevant mathematical idea, in this case, the Art Gallery problem.
The Art Gallery problem (aka the museum problem) basically asks “What is the minimum number of guards required to keep an entire region under watch?”.
We make the usual idealizing assumptions for the purposes of elegant mathematics. For instance, we assume that the guards can see infinitely far, that there are no obstructions (other than the walls), that the guards can see everything in front of them, and the like.
So looking at the map at the right, how many guards would be needed to watch over the fifth floor at the MoMA?
The Art Gallery problem is a classic question from computational geometry, and its solution involves a lot of great ideas from graph theory and graph coloring.
There are a number of fun extensions to this problems, too, including the watchmen route problem (one watchman guarding the entire museum) and the fortress problem (guarding the exterior, rather than the interior).
The Art Gallery problem is the best kind of math problem: easy to state and understand, surprisingly rich and complex, and lots of fun to play around with!
The New Scientist magazine has a monthly photo contest, and the theme this month is Geometry!
I’m thinking of submitting my picture of Parabolas in Nature, but probably not my picture of my imperfect division of a squash.
The contest ends November 30th, at midnight. The winner and select runners-up will be posted on the New Scientist website. All the details can be found here:
http://www.newscientist.com/article/dn19684-photo-competition-geometry.html
So keep your eyes open and your camera at hand–there’s a lot of Geometry out there!
This is a mind-blowing animation of arms circulating around a torus, created by Emilio Gomariz. I definitely became entranced for a bit, trying to follow a single hand all the way around the donut. (Click the image or this link if you can’t see the animation).
Apart from being visually amaazing, this puts me in mind of a result about fluid flows on surfaces. This animation demonstrates that a liquid, for example, can flow over the surface of a torus in such a way that every point moves: nothing appears stationary here, and everything is moving in a smooth (i.e., continuous) fashion.
The remarkable result is that this same can not be done on the surface of a sphere! There will always (at least) one point on the surface of the sphere that doesn’t move. A popular interpretation of this result is that however windy it might be outside, there is always at least one point on the Earth that is perfectly calm.