I really like the shape of this midtown-Manhattan sculpture. Whenever attempts are made to define or quantify beauty, symmetry is one of the first considerations. But this obtuse,scalene triangle is decidedly unsymmetric.
Maybe its lack of symmetry makes it more noticeable as a piece of public art.
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
I have written extensively about the unfaithful graphs presented on Regents exams: non-trigonometric trig functions, non-exponential exponential functions, “functions” that intersect their vertical asymptotes multiple times. I really don’t understand what is so hard about putting accurate graphs on tests.
Here is this year’s example. These are some of the ugliest “parabolas” I have ever seen. I can’t look at these without being mathematically offended.
Not one of these graphs are parabolas. Take a closer look at (3), by far the ugliest purported parabola. Look at how unparabolic this is. It lacks symmetry, and appears to turn into a line at one point!
If this were truly a parabola, we would be able to fit an isosceles triangle inside with vertex on vertex.
Not even close!
It’s a fun exercise to show that the others can’t possibly be parabolas either, which I will leave as to the reader.
Related Posts
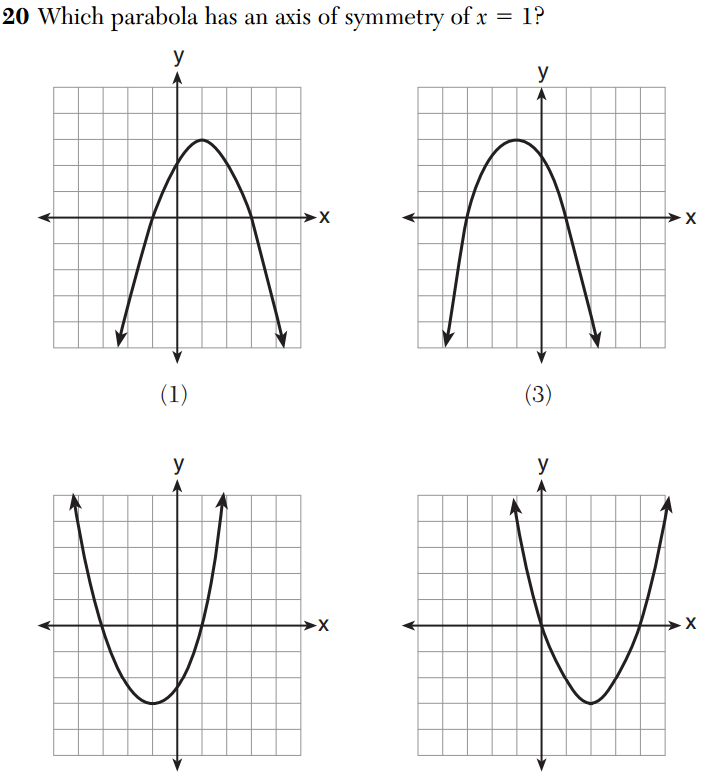
Here is another installment in my series reviewing the NY State Regents exams in mathematics.
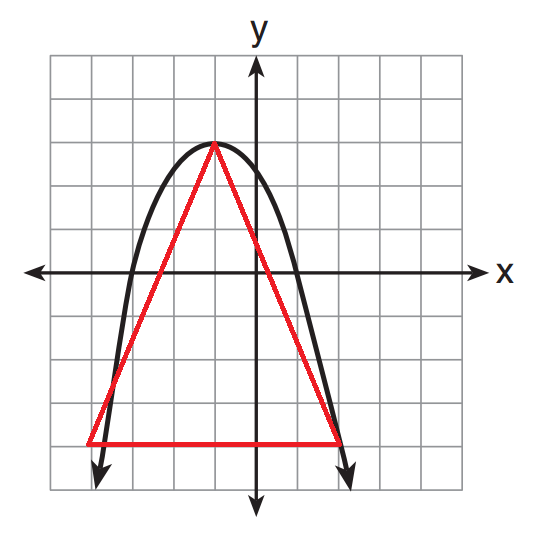
It is a true geometric wonder that a triangle’s medians always intersect at a single point. It is a remarkable and beautiful result, and the fact that the point of intersection is the centroid of the triangle makes it even more compelling.
This result should absolutely be a part of the standard Geometry curriculum. It important and beautiful mathematics, it extends a fundamental notion of mathematics (symmetry) in new ways, and it is readily accessible through folding, balancing, compass construction, and coordinate geometry.
But here’s what happens when high-stakes testing meets meaningful mathematics.
This wonderful result has been reduced to an easy-to-test trick: the centroid divides a median in a 2:1 ratio.
It’s not hard to see how such a fact can quickly become an instructional focus when it comes to centroids: if that’s how it’s going to be tested, that’s how it’s going to be taught. Of course, teachers should do more than just teach to a test, but there’s a lot riding on test results these days, and it’s hard to blame teachers for focusing on test scores when politicians, policy makers, and administrators tell them their jobs depend on it.
This is just one example of many, from one test and one state. This is an inseparable component of standardized testing, and it can be found in all content areas and at all levels. And for those who argue that the solution is simply to make better tests, keep this in mind: New York has been math Regents exams for over eighty years. Why haven’t we produced those better tests yet?
I like the many shades of grey, and the many shades of conic section, present in this spire.
I liked the look from inside the five full twists of this helical playground piece.